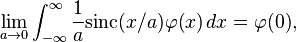Relationship To The Dirac Delta Distribution
The normalized sinc function can be used as a nascent delta function, meaning that the following weak limit holds:
This is not an ordinary limit, since the left side does not converge. Rather, it means that
for any smooth function with compact support.
In the above expression, as a approaches zero, the number of oscillations per unit length of the sinc function approaches infinity. Nevertheless, the expression always oscillates inside an envelope of ±1/(π a x), and approaches zero for any nonzero value of x. This complicates the informal picture of δ(x) as being zero for all x except at the point x = 0 and illustrates the problem of thinking of the delta function as a function rather than as a distribution. A similar situation is found in the Gibbs phenomenon.
Read more about this topic: Sinc Function
Famous quotes containing the words relationship and/or distribution:
“Friendship is by its very nature freer of deceit than any other relationship we can know because it is the bond least affected by striving for power, physical pleasure, or material profit, most liberated from any oath of duty or of constancy.”
—Francine Du Plesssix Gray (20th century)
“My topic for Army reunions ... this summer: How to prepare for war in time of peace. Not by fortifications, by navies, or by standing armies. But by policies which will add to the happiness and the comfort of all our people and which will tend to the distribution of intelligence [and] wealth equally among all. Our strength is a contented and intelligent community.”
—Rutherford Birchard Hayes (1822–1893)