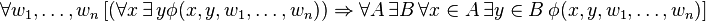Axiom Schema of Replacement - Axiom Schema of Collection

The axiom schema of collection is closely related to and frequently confused with the axiom schema of replacement. While replacement says that the image itself is a set, collection merely says that a superclass of the image is a set. In other words, the resulting set, B, is not required to be minimal.

This version of collection also lacks the uniqueness requirement on φ. Suppose that the free variables of φ are among w₁, ..., w_n, x, y; but neither A nor B is free in φ. Then the axiom schema is:

That is, the relation defined by φ is not required to be a function — some x in A may correspond to multiple y in B. In this case, the image set B whose existence is asserted must contain at least one such y for each x of the original set, with no guarantee that it will contain only one.

The axiom schema is sometimes stated without any restrictions on the predicate, φ:

In this case, there may be elements x in A that are not associated to any other sets by φ. However, the axiom schema as stated requires that, if an element x of A is associated with at least one set y, then the image set B will contain at least one such y. The resulting axiom schema is also called the axiom schema of boundedness.

The axiom schema of collection is equivalent to the axiom schema of replacement over the remainder of the ZF axioms. However, this is not so in the constructive counterpart of ZF, where Collection is stronger.