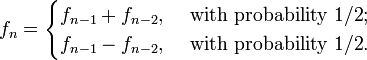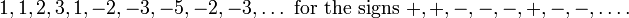Random Fibonacci Sequence - Description

Description

The random Fibonacci sequence is an integer random sequence {fn}, where f1 = f2 = 1 and the subsequent terms are determined from the random recurrence relation

f_n = \begin{cases} f_{n-1}+f_{n-2}, & \text{ with probability 1/2}; \\ f_{n-1}-f_{n-2}, & \text{ with probability 1/2}. \end{cases}

A run of the random Fibonacci sequence starts with 1,1 and the value of the each subsequent term is determined by a fair coin toss: given two consecutive elements of the sequence, the next element is either their sum or their difference with probability 1/2, independently of all the choices made previously. If in the random Fibonacci sequence the plus sign is chosen at each step, the corresponding run is the Fibonacci sequence {Fn},

If the signs alternate in minus-plus-plus-minus-plus-plus-... pattern, the result is the sequence

However, such patterns occur with vanishing probability in a random experiment. In a typical run, the terms will not follow a predictable pattern:

1, 1, 2, 3, 1, -2, -3, -5, -2, -3, \ldots \text{ for the signs } +, +, -, -, -, +, -, -, \ldots.

Similarly to the deterministic case, the random Fibonacci sequence may be profitably described via matrices:

where the signs are chosen independently for different n with equal probabilities for + or −. Thus

where {Mk} is a sequence of independent identically distributed random matrices taking values A or B with probability 1/2:

A=\begin{pmatrix} 0 & 1 \\ 1 & 1 \end{pmatrix}, \quad B=\begin{pmatrix} 0 & 1 \\ -1 & 1 \end{pmatrix}.

Read more about this topic:  Random Fibonacci Sequence

Famous quotes containing the word description:

    “The next Augustan age will dawn on the other side of the Atlantic. There will, perhaps, be a Thucydides at Boston, a Xenophon at New York, and, in time, a Virgil at Mexico, and a Newton at Peru. At last, some curious traveller from Lima will visit England and give a description of the ruins of St Paul’s, like the editions of Balbec and Palmyra.”
    —Horace Walpole (1717–1797)

    “It is possible—indeed possible even according to the old conception of logic—to give in advance a description of all ‘true’ logical propositions. Hence there can never be surprises in logic.”
    —Ludwig Wittgenstein (1889–1951)

    “The great object in life is Sensation—to feel that we exist, even though in pain; it is this “craving void” which drives us to gaming, to battle, to travel, to intemperate but keenly felt pursuits of every description whose principal attraction is the agitation inseparable from their accomplishment.”
    —George Gordon Noel Byron (1788–1824)