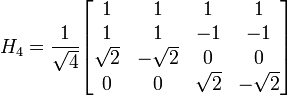Haar Wavelet - Haar Transform

The Haar transform is the simplest of the wavelet transforms. This transform cross-multiplies a function against the Haar wavelet with various shifts and stretches, like the Fourier transform cross-multiplies a function against a sine wave with two phases and many stretches.

The Haar transform is derived from the Haar matrix. An example of a 4x4 Haar transformation matrix is shown below.

H_4 = \frac{1}{\sqrt{4}} \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 1 & -1 & -1 \\ \sqrt{2} & -\sqrt{2} & 0 & 0 \\ 0 & 0 & \sqrt{2} & -\sqrt{2}\end{bmatrix}

The Haar transform can be thought of as a sampling process in which rows of the transformation matrix act as samples of finer and finer resolution.

Compare with the Walsh transform, which is also 1/–1, but is non-localized.

Read more about this topic:  Haar Wavelet

Famous quotes containing the word transform:

    “The inspired scribbler always has the gift for gossip in our common usage ... he or she can always inspire the commonplace with an uncommon flavor, and transform trivialities by some original grace or sympathy or humor or affection.”
    —Elizabeth Drew (1887–1965)