Zonal Spherical Function - Complex Case

Complex Case

If G is a complex semisimple Lie group, it is the complexification of its maximal compact subgroup K. If 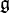and are their Lie algebras, then

Let T be a maximal torus in K with Lie algebra . Then

Let

be the Weyl group of T in K. Recall characters in Hom(T,T) are called weights and can be identified with elements of the weight lattice Λ in Hom(, R) = . There is a natural ordering on weights and very finite-dimensional irreducible representation (π, V) of K has a unique highest weight λ. The weights of the adjoint representation of K on are called roots and ρ is used to denote half the sum of the positive roots α, Weyl's character formula asserts that for z = exp X in T

where, for μ in, A_μ denotes the antisymmetrisation

and ε denotes the sign character of the finite reflection group W.

Weyl's denominator formula expresses the denominator A_ρ as a product:

where the product is over the positive roots.

Weyl's dimension formula asserts that

where the inner product on is that associated with the Killing form on .

Now

• every irreducible representation of K extends holomorphically to the complexification G

• every irreducible character χ_λ(k) of K extends holomorphically to the complexification of K and .

• for every λ in Hom(A,T) =, there is a zonal spherical function φ_λ.

The Berezin–Harish–Chandra formula asserts that for X in

In other words:

• the zonal spherical functions on a complex semisimple Lie group are given by analytic continuation of the formula for the normalised characters.

One of the simplest proofs of this formula involves the radial component on A of the Laplacian on G, a proof formally parallel to Helgason's reworking of Freudenthal's classical proof of the Weyl character formula, using the radial component on T of the Laplacian on K.

In the latter case the class functions on K can be identified with W-invariant functions on T. The radial component of Δ_K on T is just the expression for the restriction of Δ_K to W-invariant functions on T, where it is given by the formula

where

for X in . If χ is a character with highest weight λ, it follows that φ = h·χ satisfies

Thus for every weight μ with non-zero Fourier coefficient in φ,

The classical argument of Freudenthal shows that μ + ρ must have the form s(λ + ρ) for some s in W, so the character formula follows from the antisymmetry of φ.

Similarly K-biinvariant functions on G can be identified with W(A)-invariant functions on A. The radial component of Δ_G on A is just the expression for the restriction of Δ_G to W(A)-invariant functions on A. It is given by the formula

where

for X in .

The Berezin–Harish–Chandra formula for a zonal spherical function φ can be established by introducing the antisymmetric function

which is an eigenfunction of the Laplacian Δ_A. Since K is generated by copies of subgroups that are homomorphic images of SU(2) corresponding to simple roots, its complexification G is generated by the corresponding homomorphic images of SL(2,C). The formula for zonal spherical functions of SL(2,C) implies that f is a periodic function on with respect to some sublattice. Antisymmetry under the Weyl group and the argument of Freudenthal again imply that ψ must have the stated form up to a multiplicative constant, which can be determined using the Weyl dimension formula.