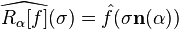Radon Transform - Relationship With The Fourier Transform

Relationship With The Fourier Transform

The Radon transform is closely related to the Fourier transform. For a function of one variable the Fourier transform is defined by

\hat{f}(\omega)=\int_{-\infty}^\infty f(x)e^{-2\pi ix\omega }\,dx.

and for a function of a 2-vector ,

\hat{f}(\mathbf{w})=\int\limits_{-\infty}^{\infty} \int\limits_{-\infty }^{\infty} f(\mathbf{x})e^{-2\pi i\mathbf{x}\cdot\mathbf{w}}\,dx\, dy.

For convenience define as it is only meaningful to take the Fourier transform in the variable. The Fourier slice theorem then states

\widehat{R_{\alpha}}(\sigma)=\hat{f}(\sigma\mathbf{n}(\alpha))

where

Thus the two-dimensional Fourier transform of the initial function is the one variable Fourier transform of the Radon transform of that function. More generally, one has the result valid in n dimensions

Indeed, the result follows at once by computing the two variable Fourier integral along appropriate slices:

An application of the Fourier inversion formula also gives an explicit inversion formula for the Radon transform, and thus shows that it is invertible on suitably chosen spaces of functions. However this form is not particularly useful for numerical inversion, and faster discrete inversion methods exist.

Read more about this topic:  Radon Transform

Famous quotes containing the words relationship with, relationship and/or transform:

    “Every man is in a state of conflict, owing to his attempt to reconcile himself and his relationship with life to his conception of harmony. This conflict makes his soul a battlefield, where the forces that wish this reconciliation fight those that do not and reject the alternative solutions they offer. Works of art are attempts to fight out this conflict in the imaginative world.”
    —Rebecca West (1892–1983)

    “The proper aim of education is to promote significant learning. Significant learning entails development. Development means successively asking broader and deeper questions of the relationship between oneself and the world. This is as true for first graders as graduate students, for fledging artists as graying accountants.”
    —Laurent A. Daloz (20th century)

    “The inspired scribbler always has the gift for gossip in our common usage ... he or she can always inspire the commonplace with an uncommon flavor, and transform trivialities by some original grace or sympathy or humor or affection.”
    —Elizabeth Drew (1887–1965)