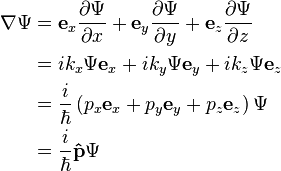Momentum Operator - Origin From de Broglie Plane Waves

Origin From De Broglie Plane Waves

The momentum and energy operators can be constructed in the following way.

One dimension

Starting in one dimension, using the plane wave solution to Schrödinger's equation:

The first order partial derivative with respect to space is

By expressing of k from the De Broglie relation:

the formula for the derivative of ψ becomes:

This suggests the operator equivalence:

so the momentum value p is a scalar factor, the momentum of the particle and the value that is measured, is the eigenvalue of the operator.

Since the partial derivative is a linear operator, the momentum operator is also linear, and because any wavefunction can be expressed as a superposition of other states, when this momentum operator acts on the entire superimposed wave, it yields the momentum eigenvalues for each plane wave component, the momenta add to the total momentum of the superimposed wave.

Three dimensions

The derivation in three dimensions is the same, except using the gradient operator del is used instead of one partial derivative. In three dimensions, the plane wave solution to Schrödinger's equation is:

and the gradient is

\begin{align} \nabla \Psi & = \bold{e}_x\frac{\partial \Psi}{\partial x} + \bold{e}_y\frac{\partial \Psi}{\partial y} + \bold{e}_z\frac{\partial \Psi}{\partial z} \\ & = i k_x\Psi\bold{e}_x + i k_y\Psi\bold{e}_y+ i k_z\Psi\bold{e}_z \\ & = \frac{i}{\hbar} \left ( p_x\bold{e}_x + p_y\bold{e}_y+ p_z\bold{e}_z \right)\Psi \\ & = \frac{i}{\hbar} \bold{\hat{p}}\Psi \\ \end{align} \,\!

where, and are the unit vectors for the three spatial dimensions, hence

This momentum operator is in position space because the partial derivatives were taken with respect to the spatial variables.

Read more about this topic:  Momentum Operator

Famous quotes containing the words origin from, origin, plane and/or waves:

    “All good poetry is the spontaneous overflow of powerful feelings: it takes its origin from emotion recollected in tranquillity.”
    —William Wordsworth (1770–1850)

    “The real, then, is that which, sooner or later, information and reasoning would finally result in, and which is therefore independent of the vagaries of me and you. Thus, the very origin of the conception of reality shows that this conception essentially involves the notion of a COMMUNITY, without definite limits, and capable of a definite increase of knowledge.”
    —Charles Sanders Peirce (1839–1914)

    “We’ve got to figure these things a little bit different than most people. Y’know, there’s something about going out in a plane that beats any other way.... A guy that washes out at the controls of his own ship, well, he goes down doing the thing that he loved the best. It seems to me that that’s a very special way to die.”
    —Dalton Trumbo (1905–1976)

    “When infant Science makes a pleasant face
    And waves again that hollow toy, the Race;”
    —Edwin Arlington Robinson (1869–1935)