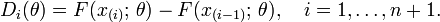Maximum Spacing Estimation - Definition

Definition

Given an iid random sample {x1, …, xn} of size n from a univariate distribution with the cumulative distribution function F(x;θ0), where θ0 ∈ Θ is an unknown parameter to be estimated, let {x(1), …, x(n)} be the corresponding ordered sample, that is the result of sorting of all observations from smallest to largest. For convenience also denote x(0) = −∞ and x(n+1) = +∞.

Define the spacings as the “gaps” between the values of the distribution function at adjacent ordered points:

D_i(\theta) = F(x_{(i)};\,\theta) - F(x_{(i-1)};\,\theta), \quad i=1,\ldots,n+1.

Then the maximum spacing estimator of θ0 is defined as a value that maximizes the logarithm of the geometric mean of sample spacings:

\hat{\theta} = \underset{\theta\in\Theta}{\operatorname{arg\,max}} \; S_n(\theta), \quad\text{where }\ S_n(\theta) = \ln\!\! \sqrt{D_1D_2\cdots D_{n+1}} = \frac{1}{n+1}\sum_{i=1}^{n+1}\ln{D_i}(\theta).

By the inequality of arithmetic and geometric means, function Sn(θ) is bounded from above by −ln(n+1), and thus the maximum has to exist at least in the supremum sense.

Note that some authors define the function Sn(θ) somewhat differently. In particular, Ranneby (1984) multiplies each Di by a factor of (n+1), whereas Cheng & Stephens (1989) omit the 1⁄n+1 factor in front of the sum and add the “−” sign in order to turn the maximization into minimization. As these are constants with respect to θ, the modifications do not alter the location of the maximum of the function Sn.

Read more about this topic:  Maximum Spacing Estimation

Famous quotes containing the word definition:

    “Scientific method is the way to truth, but it affords, even in
    principle, no unique definition of truth. Any so-called pragmatic
    definition of truth is doomed to failure equally.”
    —Willard Van Orman Quine (b. 1908)

    “According to our social pyramid, all men who feel displaced racially, culturally, and/or because of economic hardships will turn on those whom they feel they can order and humiliate, usually women, children, and animals—just as they have been ordered and humiliated by those privileged few who are in power. However, this definition does not explain why there are privileged men who behave this way toward women.”
    —Ana Castillo (b. 1953)

    “The physicians say, they are not materialists; but they are:MSpirit is matter reduced to an extreme thinness: O so thin!—But the definition of spiritual should be, that which is its own evidence. What notions do they attach to love! what to religion! One would not willingly pronounce these words in their hearing, and give them the occasion to profane them.”
    —Ralph Waldo Emerson (1803–1882)