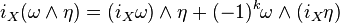Lie Derivative - The Lie Derivative of Differential Forms

The Lie Derivative of Differential Forms

The Lie derivative can also be defined on differential forms. In this context, it is closely related to the exterior derivative. Both the Lie derivative and the exterior derivative attempt to capture the idea of a derivative in different ways. These differences can be bridged by introducing the idea of an antiderivation or equivalently an interior product, after which the relationships fall out as a set of identities.

Let M be a manifold and X a vector field on M. Let be a k+1-form. The interior product of X and ω is

Note that

and that is a -antiderivation. That is, is R-linear, and

i_X (\omega \wedge \eta) = (i_X \omega) \wedge \eta + (-1)^k \omega \wedge (i_X \eta)

for and η another differential form. Also, for a function, that is a real or complex-valued function on M, one has

The relationship between exterior derivatives and Lie derivatives can then be summarized as follows. For an ordinary function f, the Lie derivative is just the contraction of the exterior derivative with the vector field X:

For a general differential form, the Lie derivative is likewise a contraction, taking into account the variation in X:

.

This identity is known variously as "Cartan's formula" or "Cartan's magic formula," and shows in particular that:

.

The derivative of products is distributed:

\mathcal{L}_{fX}\omega = f\mathcal{L}_X\omega + df \wedge i_X \omega

Read more about this topic:  Lie Derivative

Famous quotes containing the words lie, derivative, differential and/or forms:

    “When it comes to my own turn to lay my weapons down, I shall do so with thankfulness and fatigue, and whatever be my destiny afterward, I shall be glad to lie down with my fathers in honour. It is human at least, if not divine.”
    —Robert Louis Stevenson (1850–1894)

    “When we say “science” we can either mean any manipulation of the inventive and organizing power of the human intellect: or we can mean such an extremely different thing as the religion of science the vulgarized derivative from this pure activity manipulated by a sort of priestcraft into a great religious and political weapon.”
    —Wyndham Lewis (1882–1957)

    “But how is one to make a scientist understand that there is something unalterably deranged about differential calculus, quantum theory, or the obscene and so inanely liturgical ordeals of the precession of the equinoxes.”
    —Antonin Artaud (1896–1948)

    “A monarchy is the most expensive of all forms of government, the regal state requiring a costly parade, and he who depends on his own power to rule, must strengthen that power by bribing the active and enterprising whom he cannot intimidate.”
    —James Fenimore Cooper (1789–1851)