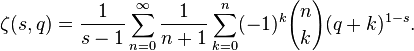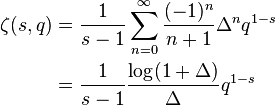Hurwitz Zeta Function - Series Representation

Series Representation

A convergent series representation defined for q > −1 and any complex s ≠ 1 was given by Helmut Hasse in 1930:

\zeta(s,q)=\frac{1}{s-1} \sum_{n=0}^\infty \frac{1}{n+1} \sum_{k=0}^n (-1)^k {n \choose k} (q+k)^{1-s}.

This series converges uniformly on compact subsets of the s-plane to an entire function. The inner sum may be understood to be the nth forward difference of ; that is,

where Δ is the forward difference operator. Thus, one may write

\begin{align} \zeta(s, q) &= \frac{1}{s-1}\sum_{n=0}^\infty \frac{(-1)^n}{n+1} \Delta^n q^{1-s}\\ &= \frac{1}{s-1} {\log(1 + \Delta) \over \Delta} q^{1-s} \end{align}

Read more about this topic:  Hurwitz Zeta Function

Famous quotes containing the word series:

    “In the order of literature, as in others, there is no act that is not the coronation of an infinite series of causes and the source of an infinite series of effects.”
    —Jorge Luis Borges (1899–1986)