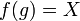Formal Power Series - Interpreting Formal Power Series As Functions

Interpreting Formal Power Series As Functions

In mathematical analysis, every convergent power series defines a function with values in the real or complex numbers. Formal power series can also be interpreted as functions, but one has to be careful with the domain and codomain. If f = ∑an Xn is an element of R], S is a commutative associative algebra over R, I is an ideal in S such that the I-adic topology on S is complete, and x is an element of I, then we can define

f(X) = \sum_{n\ge 0} a_n X^n.

This latter series is guaranteed to converge in S given the above assumptions on X. Furthermore, we have

and

Unlike in the case of bona fide functions, these formulas are not definitions but have to be proved.

Since the topology on R] is the (X)-adic topology and R] is complete, we can in particular apply power series to other power series, provided that the arguments don't have constant coefficients (so that they belong to the ideal (X)): f(0), f(X2−X) and f( (1 − X)−1 − 1) are all well defined for any formal power series f∈R].

With this formalism, we can give an explicit formula for the multiplicative inverse of a power series f whose constant coefficient a = f(0) is invertible in R:

f^{-1} = \sum_{n \ge 0} a^{-n-1} (a-f)^n.

If the formal power series g with g(0) = 0 is given implicitly by the equation

f(g) = X \,

where f is a known power series with f(0) = 0, then the coefficients of g can be explicitly computed using the Lagrange inversion formula.

Read more about this topic:  Formal Power Series

Famous quotes containing the words interpreting, formal, power, series and/or functions:

    “Drawing is a struggle between nature and the artist, in which the better the artist understands the intentions of nature, the more easily he will triumph over it. For him it is not a question of copying, but of interpreting in a simpler and more luminous language.”
    —Charles Baudelaire (1821–1867)

    “Then the justice,
    In fair round belly with good capon lined,
    With eyes severe and beard of formal cut,
    Full of wise saws and modern instances;
    And so he plays his part.”
    —William Shakespeare (1564–1616)

    “Ours is the old, old story of every uprising race or class or order. The work of elevation must be wrought by ourselves or not at all.”
    —Frances Power Cobbe (1822–1904)

    “Mortality: not acquittal but a series of postponements is what we hope for.”
    —Mason Cooley (b. 1927)

    “In today’s world parents find themselves at the mercy of a society which imposes pressures and priorities that allow neither time nor place for meaningful activities and relations between children and adults, which downgrade the role of parents and the functions of parenthood, and which prevent the parent from doing things he wants to do as a guide, friend, and companion to his children.”
    —Urie Bronfenbrenner (b. 1917)