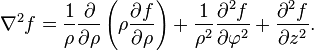Line and Volume Elements
- See multiple integral for details of volume integration in cylindrical coordinates, and Del in cylindrical and spherical coordinates for vector calculus formulae.
In many problems involving cylindrical polar coordinates, it is useful to know the line and volume elements; these are used in integration to solve problems involving paths and volumes.
The line element is
The volume element is
The surface element in a surface of constant radius (a vertical cylinder) is
The surface element in a surface of constant azimuth (a vertical half-plane) is
The surface element in a surface of constant height (a horizontal plane) is
The del operator in this system is written as
and the Laplace operator is defined by
Read more about this topic: Cylindrical Coordinate System
Famous quotes containing the words line, volume and/or elements:
“There’s something like a line of gold thread running through a man’s words when he talks to his daughter, and gradually over the years it gets to be long enough for you pick up in your hands and weave into a cloth that feels like love itself. It’s another thing, though, to hold up that cloth for inspection.”
—John Gregory Brown (20th century)
“I dare say I am compelled, unconsciously compelled, now to write volume after volume, as in past years I was compelled to go to sea, voyage after voyage. Leaves must follow upon each other as leagues used to follow in the days gone by, on and on to the appointed end, which, being Truth itself, is One—one for all men and for all occupations.”
—Joseph Conrad (1857–1924)
“The popularity of that baby-faced boy, who possessed not even the elements of a good actor, was a hallucination in the public mind, and a disgrace to our theatrical history.”
—Thomas Campbell (1777–1844)