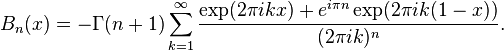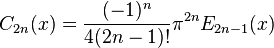Bernoulli Polynomials - Fourier Series

Fourier Series

The Fourier series of the Bernoulli polynomials is also a Dirichlet series, given by the expansion

Note the simple large n limit to suitably scaled trigonometric functions.

This is a special case of the analogous form for the Hurwitz zeta function

B_n(x) = -\Gamma(n+1) \sum_{k=1}^\infty \frac{ \exp (2\pi ikx) + e^{i\pi n} \exp (2\pi ik(1-x)) } { (2\pi ik)^n }.

This expansion is valid only for 0 ≤ x ≤ 1 when n ≥ 2 and is valid for 0 < x < 1 when n = 1.

The Fourier series of the Euler polynomials may also be calculated. Defining the functions

C_\nu(x) = \sum_{k=0}^\infty \frac {\cos((2k+1)\pi x)} {(2k+1)^\nu}

and

S_\nu(x) = \sum_{k=0}^\infty \frac {\sin((2k+1)\pi x)} {(2k+1)^\nu}

for, the Euler polynomial has the Fourier series

C_{2n}(x) = \frac{(-1)^n}{4(2n-1)!} \pi^{2n} E_{2n-1} (x)

and

S_{2n+1}(x) = \frac{(-1)^n}{4(2n)!} \pi^{2n+1} E_{2n} (x).

Note that the and are odd and even, respectively:

and

They are related to the Legendre chi function as

and

Read more about this topic:  Bernoulli Polynomials

Famous quotes containing the word series:

    “Depression moods lead, almost invariably, to accidents. But, when they occur, our mood changes again, since the accident shows we can draw the world in our wake, and that we still retain some degree of power even when our spirits are low. A series of accidents creates a positively light-hearted state, out of consideration for this strange power.”
    —Jean Baudrillard (b. 1929)