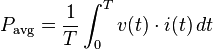Audio Power - Power Calculations

Power Calculations

Since the instantaneous power of an AC waveform varies over time, AC power, which includes audio power, is typically measured as an average over time. It is based on this formula:

P_\mathrm{avg} = \frac{1}{T}\int_{0}^{T} v(t) \cdot i(t)\, dt \,

For a purely resistive load, a simpler equation can be used, based on the root mean square (RMS) values of the voltage and current waveforms:

P_\mathrm{avg} = V_\mathrm{rms} \cdot I_\mathrm{rms} \,

In the case of a steady sinusoidal tone (not music) into a purely resistive load, this can be calculated from the peak amplitude of the voltage waveform (which is easier to measure with an oscilloscope) and the load's resistance:

V_\mathrm{rms} \cdot I_\mathrm{rms} = \frac{V_\mathrm{rms}^2}{R} = \frac{V_\mathrm{peak}^2}{2R} \,

Though a speaker is not purely resistive, these equations are often used to approximate power measurements for such a system.

Read more about this topic:  Audio Power

Famous quotes containing the words power and/or calculations:

    “We should seek by all means in our power to avoid war, by analysing possible causes, by trying to remove them, by discussion in a spirit of collaboration and good will. I cannot believe that such a programme would be rejected by the people of this country, even if it does mean the establishment of personal contact with the dictators.”
    —Neville Chamberlain (1869–1940)

    “He who is conversant with the supernal powers will not worship these inferior deities of the wind, waves, tide, and sunshine. But we would not disparage the importance of such calculations as we have described. They are truths in physics because they are true in ethics.”
    —Henry David Thoreau (1817–1862)