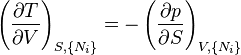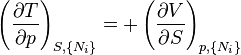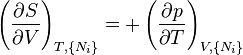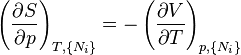Thermodynamic Potential - The Maxwell Relations

The Maxwell Relations

Again, define and to be conjugate pairs, and the to be the natural variables of some potential . We may take the "cross differentials" of the state equations, which obey the following relationship:

$\left(\frac{\partial}{\partial y_j} \left(\frac{\partial \Phi}{\partial y_k} \right)_{\{y_{i\ne k}\}} \right)_{\{y_{i\ne j}\}} = \left(\frac{\partial}{\partial y_k} \left(\frac{\partial \Phi}{\partial y_j} \right)_{\{y_{i\ne j}\}} \right)_{\{y_{i\ne k}\}}$

From these we get the Maxwell relations. There will be (D-1)/2 of them for each potential giving a total of D(D-1)/2 equations in all. If we restrict ourselves the U, F, H, G

$\left(\frac{\partial T}{\partial V}\right)_{S,\{N_i\}} = -\left(\frac{\partial p}{\partial S}\right)_{V,\{N_i\}}$

$\left(\frac{\partial T}{\partial p}\right)_{S,\{N_i\}} = +\left(\frac{\partial V}{\partial S}\right)_{p,\{N_i\}}$

$\left(\frac{\partial S}{\partial V}\right)_{T,\{N_i\}} = +\left(\frac{\partial p}{\partial T}\right)_{V,\{N_i\}}$

$\left(\frac{\partial S}{\partial p}\right)_{T,\{N_i\}} = -\left(\frac{\partial V}{\partial T}\right)_{p,\{N_i\}}$

Using the equations of state involving the chemical potential we get equations such as:

$\left(\frac{\partial T}{\partial N_j}\right)_{V,S,\{N_{i\ne j}\}} = \left(\frac{\partial \mu_j}{\partial S}\right)_{V,\{N_i\}}$

and using the other potentials we can get equations such as:

$\left(\frac{\partial N_j}{\partial V}\right)_{S,\mu_j,\{N_{i\ne j}\}} = -\left(\frac{\partial p}{\partial \mu_j}\right)_{S,V\{N_{i\ne j}\}}$

$\left(\frac{\partial N_j}{\partial N_k}\right)_{S,V,\mu_j,\{N_{i\ne j,k}\}} = -\left(\frac{\partial \mu_k}{\partial \mu_j}\right)_{S,V\{N_{i\ne j}\}}$

Read more about this topic: Thermodynamic Potential

Famous quotes containing the words maxwell and/or relations:

“Poopsie, you’re just an eight-ball with hips.”
—Griffin Jay, Maxwell Shane (1905–1983)

“When one walks, one is brought into touch first of all with the essential relations between one’s physical powers and the character of the country; one is compelled to see it as its natives do. Then every man one meets is an individual. One is no longer regarded by the whole population as an unapproachable and uninteresting animal to be cheated and robbed.”
—Aleister Crowley (1875–1947)