Roulette - Mathematical Model

Mathematical Model

As an example, we can examine the European roulette model (roulette with one zero). Since this roulette has 37 cells with equal odds of hitting, it is clear that this is a final model of field probability, where, for all . We'll call the bet a three, where for a certain random event|event, and = random size. The event naturally leads to a winning event, to the size of the bet (in dollars, for example), to the bet rule, and the mathematical expectation relates to the bet profitability.

The rules of European roulette have 10 types of bets. First we can examine the 'Straight Up' bet. It's clear that in this case, where, and is determined by this law

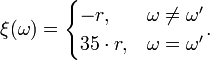
\xi(\omega) = \begin{cases} -r, &\omega \ne \omega^\prime\\ 35 \cdot r, &\omega = \omega^\prime \end{cases}.


The bet's probability is equal to

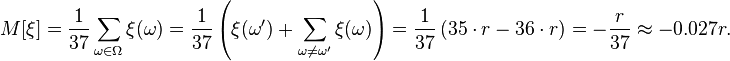
M = \frac{1}{37} \sum_{\omega \in \Omega} \xi(\omega) = \frac{1}{37} \left(\xi(\omega^\prime) + \sum_{\omega \ne \omega^\prime} \xi(\omega)\right) = \frac{1}{37} \left(35 \cdot r - 36 \cdot r \right) = -\frac{r}{37} \approx -0.027r.


Without details, for a bet, black (or red), the rule is determined as

\xi(\omega) = \begin{cases} -r, &\omega \text{ is red} \\ -r, &\omega = 0 \\ r, &\omega \text{ is black} \end{cases},


and the profitability . For similar reasons it is simple to see that the profitability is also equal for all remaining types of bets. .

In reality this means that, the more bets a player makes, the more he is going to lose independent of the strategies (combinations of bet types or size of bets) that he employs:


Here, the profit margin for the roulette owner is equal to approximately 2.7%. Nevertheless, several roulette strategy systems have been developed despite the losing odds. These systems can not change the odds of the game in favor of the player.

It's worth noting that the odds for the player in American roulette are even worse, as the bet profitability is at worst, and never better than .


Read more about this topic:  Roulette

Famous quotes containing the words mathematical and/or model:

    “It is by a mathematical point only that we are wise, as the sailor or the fugitive slave keeps the polestar in his eye; but that is sufficient guidance for all our life. We may not arrive at our port within a calculable period, but we would preserve the true course.”
    —Henry David Thoreau (1817–1862)

    “The Battle of Waterloo is a work of art with tension and drama with its unceasing change from hope to fear and back again, change which suddenly dissolves into a moment of extreme catastrophe, a model tragedy because the fate of Europe was determined within this individual fate.”
    —Stefan Zweig (18811942)