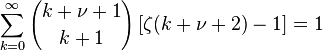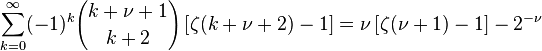Rational Zeta Series - Polygamma-related Series

Polygamma-related Series

A number of additional relationships can be derived from the Taylor series for the polygamma function at z = 1, which is

\psi^{(m)}(z+1)= \sum_{k=0}^\infty (-1)^{m+k+1} (m+k)!\; \zeta (m+k+1)\; \frac {z^k}{k!}.

The above converges for |z| < 1. A special case is

\sum_{n=2}^\infty t^n \left = -t\left

which holds for |t| < 2. Here, ψ is the digamma function and ψ(m) is the polygamma function. Many series involving the binomial coefficient may be derived:

\sum_{k=0}^\infty {k+\nu+1 \choose k} \left = \zeta(\nu+2)

where ν is a complex number. The above follows from the series expansion for the Hurwitz zeta

\zeta(s,x+y) = \sum_{k=0}^\infty {s+k-1 \choose s-1} (-y)^k \zeta (s+k,x)

taken at y = −1. Similar series may be obtained by simple algebra:

\sum_{k=0}^\infty {k+\nu+1 \choose k+1} \left = 1

and

\sum_{k=0}^\infty (-1)^k {k+\nu+1 \choose k+1} \left = 2^{-(\nu+1)}

and

\sum_{k=0}^\infty (-1)^k {k+\nu+1 \choose k+2} \left = \nu \left - 2^{-\nu}

and

\sum_{k=0}^\infty (-1)^k {k+\nu+1 \choose k} \left = \zeta(\nu+2)-1 - 2^{-(\nu+2)}

For integer n ≥ 0, the series

can be written as the finite sum

The above follows from the simple recursion relation Sn + Sn + 1 = ζ(n + 2). Next, the series

may be written as

for integer n ≥ 1. The above follows from the identity Tn + Tn + 1 = Sn. This process may be applied recursively to obtain finite series for general expressions of the form

for positive integers m.

Read more about this topic:  Rational Zeta Series

Famous quotes containing the word series:

    “I look on trade and every mechanical craft as education also. But let me discriminate what is precious herein. There is in each of these works an act of invention, an intellectual step, or short series of steps taken; that act or step is the spiritual act; all the rest is mere repetition of the same a thousand times.”
    —Ralph Waldo Emerson (1803–1882)