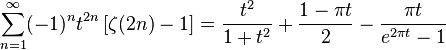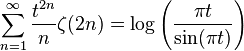Rational Zeta Series - Elementary Series

Elementary Series

For integer m, one has

For m=2, a number of interesting numbers have a simple expression as rational zeta series:

and

where γ is the Euler–Mascheroni constant. The series

follows by summing the Gauss–Kuzmin distribution. There are also series for π:

and

being notable because of its fast convergence. This last series follows from the general identity

\sum_{n=1}^\infty (-1)^{n} t^{2n} \left = \frac{t^2}{1+t^2} + \frac{1-\pi t}{2} - \frac {\pi t}{e^{2\pi t} -1}

which in turn follows from the generating function for the Bernoulli numbers

Adamchik and Srivastava give a similar series

\sum_{n=1}^\infty \frac{t^{2n}}{n} \zeta(2n) = \log \left(\frac{\pi t} {\sin (\pi t)}\right)

Read more about this topic:  Rational Zeta Series

Famous quotes containing the words elementary and/or series:

    “If men as individuals surrender to the call of their elementary instincts, avoiding pain and seeking satisfaction only for their own selves, the result for them all taken together must be a state of insecurity, of fear, and of promiscuous misery.”
    —Albert Einstein (1879–1955)

    “The woman’s world ... is shown as a series of limited spaces, with the woman struggling to get free of them. The struggle is what the film is about; what is struggled against is the limited space itself. Consequently, to make its point, the film has to deny itself and suggest it was the struggle that was wrong, not the space.”
    —Jeanine Basinger (b. 1936)