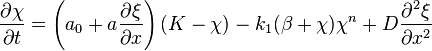Brian Goodwin - Models in Developmental Biology

Models in Developmental Biology

Later on, he explored the problem of self-organization in pattern formation, using different case studies, from single-cell organisms (as Acetabularia) to multicellular organisms, including early development in Drosophila. One of his key contributions was to link morphogenetic fields, defined in terms of spatial distributions of chemical signals (morphogenes), and the shape of the system experiencing morphogenetic changes. In this way, geometry and development were linked through a mathematical formalism. Along with his colleague Lynn Trainor, Goodwin developed a set of mathematical equations describing the changes of both physical boundaries in the organism and chemical gradients.

By considering the mechanochemical behaviour of the cortical cytoplasm (or cytogel) of plant cells, a viscoelastic material mainly composed of actin microfilaments and reinforced by a microtubules network, Goodwin & Trainor (1985) showed how to couple calcium and the mechanical properties of the cytoplasm. The cytogel is treated as a continuous viscoelastic medium in which calcium ions can diffuse and interact with the cytoskeleton. The model consists in two non-linear partial differential equations which describe the evolution of the mechanical strain field and .of the calcium distribution in the cytogel.

It has been shown (Trainor & Goodwin, 1986) that, in a range of parameter values, instabilities may occur and develop in this system, leading to intracellular patterns of strain and calcium concentration. The equations read, in their general form:

\rho {\partial^2 \xi \over \partial t^2} = {\partial \over \partial x} \left ( P_1(\chi){\partial \xi \over \partial x} \right ) + {\partial \over \partial x} \left ( P_2(\chi){\partial^2 \xi \over \partial x \partial t} \right ) - P_3(\chi) - F_0 {\partial \chi \over \partial x}
{\partial \chi \over \partial t} = \left ( a_0 + a {\partial \xi \over \partial x} \right ) (K-\chi) - k_1(\beta+\chi)\chi^n + D {\partial^2 \xi \over \partial x^2}

These equations describe the spatiotemporal dynamics of the displacement from the reference state and the calcium concentration, respectively. Here x and t are the space and time coordinates, respectively. These equations can be applied to many different scenarios and the different functions P(x) introduce the specific mechanical properties of the medium. These equations are very rich in terms of the static and dynamic patterns that can generate, including both complex geometrical motifs to oscillations and chaos (Briere 1994).

Read more about this topic:  Brian Goodwin

Famous quotes containing the words models and/or biology:

    “French rhetorical models are too narrow for the English tradition. Most pernicious of French imports is the notion that there is no person behind a text. Is there anything more affected, aggressive, and relentlessly concrete than a Parisan intellectual behind his/her turgid text? The Parisian is a provincial when he pretends to speak for the universe.”
    —Camille Paglia (b. 1947)

    “The “control of nature” is a phrase conceived in arrogance, born of the Neanderthal age of biology and the convenience of man.”
    —Rachel Carson (1907–1964)