Zech's Logarithms - Examples

Examples

Let α ∈ GF(23) be a root of the primitive polynomial x3 + x2 + 1. The traditional representation of elements of this field is as polynomials in α of degree 2 or less.

A table of Zech logarithms for this field are Z(-∞)=0, Z(0)=-∞, Z(1)=5, Z(2)=3, Z(3)=2, Z(4)=6, Z(5)=1, and Z(6)=4. The multiplicative order of α is 7, so the exponential representation works with integers modulo 7.

Since α is a root of x3 + x2 + 1 then that means α3 + α2 + 1 = 0, or if we recall that since all coefficients are in GF(2), subtraction is the same as addition, we obtain α3 = α2 + 1.

The conversion from exponential to polynomial representations is given by

\alpha^3 = \alpha^2 + 1 (as shown above)
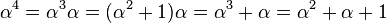
\alpha^4 = \alpha^3 \alpha = (\alpha^2 + 1)\alpha = \alpha^3 + \alpha = \alpha^2 + \alpha + 1
\alpha^5 = \alpha^4 \alpha = (\alpha^2 + \alpha + 1)\alpha = \alpha^3 + \alpha^2 + \alpha = \alpha^2 + 1 + \alpha^2 + \alpha = \alpha + 1
\alpha^6 = \alpha^5 \alpha = (\alpha + 1)\alpha = \alpha^2 + \alpha

Using Zech logarithms to compute α6 + α3:

and verifying it in the polynomial representation:

Read more about this topic:  Zech's Logarithms

Famous quotes containing the word examples:

    “In the examples that I here bring in of what I have [read], heard, done or said, I have refrained from daring to alter even the smallest and most indifferent circumstances. My conscience falsifies not an iota; for my knowledge I cannot answer.”
    —Michel de Montaigne (1533–1592)

    “Histories are more full of examples of the fidelity of dogs than of friends.”
    —Alexander Pope (1688–1744)

    “There are many examples of women that have excelled in learning, and even in war, but this is no reason we should bring ‘em all up to Latin and Greek or else military discipline, instead of needle-work and housewifry.”
    —Bernard Mandeville (1670–1733)