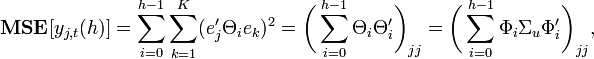Variance Decomposition - Calculating The Forecast Error Variance

Calculating The Forecast Error Variance

For the VAR (p) of form

$y_t=\nu +A_1y_{t-1}+\dots+A_p y_{t-p}+u_t$ .

This can be changed to a VAR(1) structure by writing it in companion form (see general matrix notation of a VAR(p))

$Y_t=\mathbf{\nu} +A Y_{t-1}+U_t$ where

$A=\begin{bmatrix} A_1 & A_2 & \dots & A_{p-1} & A_p \\ \mathbf{I}_k & 0 & \dots & 0 & 0 \\ 0 & \mathbf{I}_k & & 0 & 0 \\ \vdots & & \ddots & \vdots & \vdots \\ 0 & 0 & \dots & \mathbf{I}_k & 0 \\ \end{bmatrix}$ , $Y=\begin{bmatrix} y_1 \\ \vdots \\ y_p \end{bmatrix}$ , $V=\begin{bmatrix} \nu \\ 0 \\ \vdots \\ 0 \end{bmatrix}$ and $U_t=\begin{bmatrix} u_t \\ 0 \\ \vdots \\ 0 \end{bmatrix}$

where, and are dimensional column vectors, is by dimensional matrix and, and are dimensional column vectors.

The mean squared error of the h-step forecast of variable j is, where

$\mathbf{MSE}=\sum_{i=0}^{h-1}\sum_{k=1}^{K}(e_j'\Theta_ie_k)^2=\bigg(\sum_{i=0}^{h-1}\Theta_i\Theta_i'\bigg)_{jj}=\bigg(\sum_{i=0}^{h-1}\Phi_i\Sigma_u\Phi_i'\bigg)_{jj},$

and where

is the jth column of and the subscript refers to that element of the matrix

where is a lower triangular matrix obtained by a Cholesky decomposition of such that, where is the covariance matrix of the errors

where $J=\begin{bmatrix} \mathbf{I}_k &0 & \dots & 0\end{bmatrix} ,$ so that is a by dimensional matrix.

The amount of forecast error variance of variable accounted for by exogenous shocks to variable is given by

$\omega_{jk,h}=\sum_{i=0}^{h-1}(e_j'\Theta_ie_k)^2/MSE .$

Read more about this topic: Variance Decomposition

Famous quotes containing the words calculating the, calculating, forecast, error and/or variance:

“[The] elderly and timid single gentleman in Paris ... never drove down the Champs Elysees without expecting an accident, and commonly witnessing one; or found himself in the neighborhood of an official without calculating the chances of a bomb. So long as the rates of progress held good, these bombs would double in force and number every ten years.”
—Henry Brooks Adams (1838–1918)

“What our children have to fear is not the cars on the highways of tomorrow but our own pleasure in calculating the most elegant parameters of their deaths.”
—J.G. (James Graham)

“I cannot forecast to you the action of Russia. It is a riddle wrapped in a mystery inside an enigma.”
—Winston Churchill (1874–1965)

“Still we live meanly, like ants; though the fable tells us that we were long ago changed into men; like pygmies we fight with cranes; it is error upon error, and clout upon clout, and our best virtue has for its occasion a superfluous and evitable wretchedness. Our life is frittered away by detail.”
—Henry David Thoreau (1817–1862)

“There is an untroubled harmony in everything, a full consonance in nature; only in our illusory freedom do we feel at variance with it.”
—Fyodor Tyutchev (1803–1873)