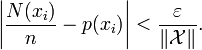Strongly Typical Sequences (strong Typicality, Letter Typicality)
If a sequence x1, ..., xn is drawn from some specified joint distribution defined over a finite or an infinite alphabet, then the strongly typical set, Aε,strong(n) is defined as the set of sequences which satisfy
where is the number of occurrences of a specific symbol in the sequence.
It can be shown that strongly typical sequences are also weakly typical (with a different constant ε), and hence the name. The two forms, however, are not equivalent. Strong typicality is often easier to work with in proving theorems for memoryless channels. However, as is apparent from the definition, this form of typicality is only defined for random variables having finite support.
Read more about this topic: Typical Set
Famous quotes containing the words strongly, typical and/or letter:
“I feel that any form of so called psychotherapy is strongly contraindicated for addicts.... The question “Why did you start using narcotics in the first place?” should never be asked. It is quite as irrelevant to treatment as it would be to ask a malarial patient why he went to a malarial area.”
—William Burroughs (b. 1914)
“Sinclair Lewis is the perfect example of the false sense of time of the newspaper world.... [ellipsis in source] He was always dominated by an artificial time when he wrote Main Street.... He did not create actual human beings at any time. That is what makes it newspaper. Sinclair Lewis is the typical newspaperman and everything he says is newspaper. The difference between a thinker and a newspaperman is that a thinker enters right into things, a newspaperman is superficial.”
—Gertrude Stein (1874–1946)
“To know the laws is not to memorize their letter but to grasp their full force and meaning.”
—Marcus Tullius Cicero (106–43 B.C.)