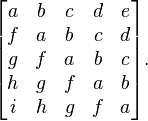Toeplitz Matrix

In linear algebra, a Toeplitz matrix or diagonal-constant matrix, named after Otto Toeplitz, is a matrix in which each descending diagonal from left to right is constant. For instance, the following matrix is a Toeplitz matrix:

\begin{bmatrix} a & b & c & d & e \\ f & a & b & c & d \\ g & f & a & b & c \\ h & g & f & a & b \\ i & h & g & f & a \end{bmatrix}.

Any n×n matrix A of the form

A = \begin{bmatrix} a_{0} & a_{-1} & a_{-2} & \ldots & \ldots &a_{-n+1} \\ a_{1} & a_0 & a_{-1} & \ddots & & \vdots \\ a_{2} & a_{1} & \ddots & \ddots & \ddots& \vdots \\ \vdots & \ddots & \ddots & \ddots & a_{-1} & a_{-2}\\ \vdots & & \ddots & a_{1} & a_{0}& a_{-1} \\ a_{n-1} & \ldots & \ldots & a_{2} & a_{1} & a_{0} \end{bmatrix}

is a Toeplitz matrix. If the i,j element of A is denoted Ai,j, then we have

Read more about Toeplitz Matrix:  Solving A Toeplitz System, General Properties, Discrete Convolution

Famous quotes containing the word matrix:

    “As all historians know, the past is a great darkness, and filled with echoes. Voices may reach us from it; but what they say to us is imbued with the obscurity of the matrix out of which they come; and try as we may, we cannot always decipher them precisely in the clearer light of our day.”
    —Margaret Atwood (b. 1939)