Thirring Model - Definition

Definition

The Thirring model is given by the Lagrangian density

$\mathcal{L}= \overline{\psi}(i\partial\!\!\!/-m)\psi -\frac{g}{2}\left(\overline{\psi}\gamma^\mu\psi\right) \left(\overline{\psi}\gamma_\mu \psi\right)\$

where is the field, g is the coupling constant, m is the mass, and, for, are the two-dimensional gamma matrices.

This is the unique model of (1+1)-dimensional, Dirac fermions with a local (self-)interaction. Indeed, since there are only 4 independent fields, because of the Pauli principle, all the quartic, local interactions are equivalent; and all higher power, local interactions vanish. (Interactions containing derivatives, such as 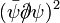$(\bar \psi\partial\!\!\!/\psi)^2$ , are not considered because they are non-renormalizable.)

The correlation functions of the Thirring model (massive or massless) verify the Osterwalder-Schrader axioms, and hence the theory makes sense as a quantum field theory.

Read more about this topic: Thirring Model

Famous quotes containing the word definition:

“According to our social pyramid, all men who feel displaced racially, culturally, and/or because of economic hardships will turn on those whom they feel they can order and humiliate, usually women, children, and animals—just as they have been ordered and humiliated by those privileged few who are in power. However, this definition does not explain why there are privileged men who behave this way toward women.”
—Ana Castillo (b. 1953)

“... we all know the wag’s definition of a philanthropist: a man whose charity increases directly as the square of the distance.”
—George Eliot [Mary Ann (or Marian)

“I’m beginning to think that the proper definition of “Man” is “an animal that writes letters.””
—Lewis Carroll [Charles Lutwidge Dodgson] (1832–1898)