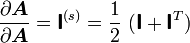Tensor Derivative (continuum Mechanics) - Derivative of A Second-order Tensor With Respect To Itself

Derivative of A Second-order Tensor With Respect To Itself

Let be a second order tensor. Then

$\frac{\partial \boldsymbol{A}}{\partial \boldsymbol{A}}:\boldsymbol{T} = \left_{\alpha = 0} = \boldsymbol{T} = \boldsymbol{\mathsf{I}}:\boldsymbol{T}$

Therefore,

$\frac{\partial \boldsymbol{A}}{\partial \boldsymbol{A}} = \boldsymbol{\mathsf{I}}$

Here is the fourth order identity tensor. In index notation with respect to an orthonormal basis

$\boldsymbol{\mathsf{I}} = \delta_{ik}~\delta_{jl}~\mathbf{e}_i\otimes\mathbf{e}_j\otimes\mathbf{e}_k\otimes\mathbf{e}_l$

This result implies that

$\frac{\partial \boldsymbol{A}^T}{\partial \boldsymbol{A}}:\boldsymbol{T} = \boldsymbol{\mathsf{I}}^T:\boldsymbol{T} = \boldsymbol{T}^T$

where

$\boldsymbol{\mathsf{I}}^T = \delta_{jk}~\delta_{il}~\mathbf{e}_i\otimes\mathbf{e}_j\otimes\mathbf{e}_k\otimes\mathbf{e}_l$

Therefore, if the tensor is symmetric, then the derivative is also symmetric and we get

$\frac{\partial \boldsymbol{A}}{\partial \boldsymbol{A}} = \boldsymbol{\mathsf{I}}^{(s)} = \frac{1}{2}~(\boldsymbol{\mathsf{I}} + \boldsymbol{\mathsf{I}}^T)$

where the symmetric fourth order identity tensor is

$\boldsymbol{\mathsf{I}}^{(s)} = \frac{1}{2}~(\delta_{ik}~\delta_{jl} + \delta_{il}~\delta_{jk}) ~\mathbf{e}_i\otimes\mathbf{e}_j\otimes\mathbf{e}_k\otimes\mathbf{e}_l$

Read more about this topic: Tensor Derivative (continuum Mechanics)

Famous quotes containing the words derivative and/or respect:

“When we say “science” we can either mean any manipulation of the inventive and organizing power of the human intellect: or we can mean such an extremely different thing as the religion of science the vulgarized derivative from this pure activity manipulated by a sort of priestcraft into a great religious and political weapon.”
—Wyndham Lewis (1882–1957)

“Writing, when properly managed ... is but a different name for conversation: As no one ... would venture to talk all;Mso no author, who understands the just boundaries of decorum and good breeding, would presume to think all: The truest respect which you can pay to the reader’s understanding, is to ... leave him something to imagine, in his turn, as well as yourself.”
—Laurence Sterne (1713–1768)