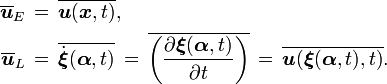Stokes Drift - Mathematical Description

Mathematical Description

The Lagrangian motion of a fluid parcel with position vector x = ξ(α,t) in the Eulerian coordinates is given by:

\dot{\boldsymbol{\xi}}\, =\, \frac{\partial \boldsymbol{\xi}}{\partial t}\, =\, \boldsymbol{u}(\boldsymbol{\xi},t),

where ∂ξ / ∂t is the partial derivative of ξ(α,t) with respect to t, and

ξ(α,t) is the Lagrangian position vector of a fluid parcel, in meters,
u(x,t) is the Eulerian velocity, in meters per second,
x is the position vector in the Eulerian coordinate system, in meters,
α is the position vector in the Lagrangian coordinate system, in meters,
t is the time, in seconds.

Often, the Lagrangian coordinates α are chosen to coincide with the Eulerian coordinates x at the initial time t = t0 :

\boldsymbol{\xi}(\boldsymbol{\alpha},t_0)\, =\, \boldsymbol{\alpha}.

But also other ways of labeling the fluid parcels are possible.

If the average value of a quantity is denoted by an overbar, then the average Eulerian velocity vector ūE and average Lagrangian velocity vector ūL are:

\begin{align} \overline{\boldsymbol{u}}_E\, &=\, \overline{\boldsymbol{u}(\boldsymbol{x},t)}, \\ \overline{\boldsymbol{u}}_L\, &=\, \overline{\dot{\boldsymbol{\xi}}(\boldsymbol{\alpha},t)}\, =\, \overline{\left(\frac{\partial \boldsymbol{\xi}(\boldsymbol{\alpha},t)}{\partial t}\right)}\, =\, \overline{\boldsymbol{u}(\boldsymbol{\xi}(\boldsymbol{\alpha},t),t)}. \end{align}

Different definitions of the average may be used, depending on the subject of study, see ergodic theory:

  • time average,
  • space average,
  • ensemble average and
  • phase average.

Now, the Stokes drift velocity ūS equals

\overline{\boldsymbol{u}}_S\, =\, \overline{\boldsymbol{u}}_L\, -\, \overline{\boldsymbol{u}}_E.

In many situations, the mapping of average quantities from some Eulerian position x to a corresponding Lagrangian position α forms a problem. Since a fluid parcel with label α traverses along a path of many different Eulerian positions x, it is not possible to assign α to a unique x. A mathematical sound basis for an unambiguous mapping between average Lagrangian and Eulerian quantities is provided by the theory of the Generalized Lagrangian Mean (GLM) by Andrews and McIntyre (1978).

Read more about this topic:  Stokes Drift

Famous quotes containing the words mathematical and/or description:

    “All science requires mathematics. The knowledge of mathematical things is almost innate in us.... This is the easiest of sciences, a fact which is obvious in that no one’s brain rejects it; for laymen and people who are utterly illiterate know how to count and reckon.”
    —Roger Bacon (c. 1214–c. 1294)

    “I was here first introduced to Joe.... He was a good-looking Indian, twenty-four years old, apparently of unmixed blood, short and stout, with a broad face and reddish complexion, and eyes, methinks, narrower and more turned up at the outer corners than ours, answering to the description of his race. Besides his underclothing, he wore a red flannel shirt, woolen pants, and a black Kossuth hat, the ordinary dress of the lumberman, and, to a considerable extent, of the Penobscot Indian.”
    —Henry David Thoreau (1817–1862)