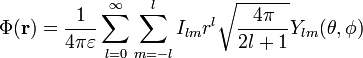Spherical Multipole Moments - Interior Spherical Multipole Moments

Interior Spherical Multipole Moments

Similarly, the interior multipole expansion has the same functional form

$\Phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon} \sum_{l=0}^{\infty} \sum_{m=-l}^{l} I_{lm} r^{l} \sqrt{\frac{4\pi}{2l+1}} Y_{lm}(\theta, \phi)$

with the interior multipole moments defined as

$I_{lm} \ \stackrel{\mathrm{def}}{=}\ \int d\mathbf{r}^{\prime} \frac{\rho(\mathbf{r}^{\prime})}{\left( r^{\prime} \right)^{l+1}} \sqrt{\frac{4\pi}{2l+1}} Y_{lm}^{*}(\theta^{\prime}, \phi^{\prime})$

Read more about this topic: Spherical Multipole Moments

Famous quotes containing the words interior and/or moments:

“Or would interior time, that could delay
The sentence chronic with the last assize,
Start running backwards with its timely lies,
I might have time to live the love I say....”
—Allen Tate (1899–1979)

“There are moments when very little truth would be enough to shape opinion. One might be hated at extremely low cost.”
—Jean Rostand (1894–1977)