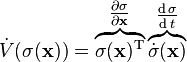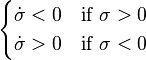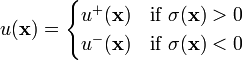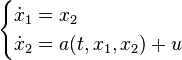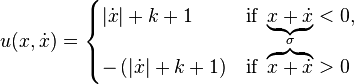Sliding Mode Control - Control Design Examples

Control Design Examples

  • Consider a plant described by Equation (1) with single input (i.e., ). The switching function is picked to be the linear combination
\sigma(\mathbf{x}) \triangleq s_1 x_1 + s_2 x_2 + \cdots + s_{n-1} x_{n-1} + s_n x_n
where the weight for all . The sliding surface is the simplex where . When trajectories are forced to slide along this surface,
and so
which is a reduced-order system (i.e., the new system is of order because the system is constrained to this -dimensional sliding mode simplex). This surface may have favorable properties (e.g., when the plant dynamics are forced to slide along this surface, they move toward the origin ). Taking the derivative of the Lyapunov function in Equation (3), we have
\dot{V}(\sigma(\mathbf{x})) = \overbrace{\sigma(\mathbf{x})^{\text{T}}}^{\tfrac{\partial \sigma}{\partial \mathbf{x}}} \overbrace{\dot{\sigma}(\mathbf{x})}^{\tfrac{\operatorname{d} \sigma}{\operatorname{d} t}}
To ensure is a negative-definite function (i.e., for Lyapunov stability of the surface ), the feedback control law must be chosen so that
\begin{cases} \dot{\sigma} < 0 &\text{if } \sigma > 0\\ \dot{\sigma} > 0 &\text{if } \sigma < 0 \end{cases}
Hence, the product because it is the product of a negative and a positive number. Note that
\dot{\sigma}(\mathbf{x}) = \overbrace{\frac{\partial{\sigma(\mathbf{x})}}{\partial{\mathbf{x}}} \dot{\mathbf{x}}}^{\dot{\sigma}(\mathbf{x})} = \frac{\partial{\sigma(\mathbf{x})}}{\partial{\mathbf{x}}} \overbrace{\left( f(\mathbf{x},t) + B(\mathbf{x},t) u \right)}^{\dot{\mathbf{x}}} = \overbrace{}^{\frac{\partial{\sigma(\mathbf{x})}}{\partial{\mathbf{x}}}} \underbrace{\overbrace{\left( f(\mathbf{x},t) + B(\mathbf{x},t) u \right)}^{\dot{\mathbf{x}}}}_{\text{( i.e., an } n \times 1 \text{ vector )}}
The control law is chosen so that
u(\mathbf{x}) = \begin{cases} u^+(\mathbf{x}) &\text{if } \sigma(\mathbf{x}) > 0 \\ u^-(\mathbf{x}) &\text{if } \sigma(\mathbf{x}) < 0 \end{cases}
where
  • is some control (e.g., possibly extreme, like "on" or "forward") that ensures Equation (5) (i.e., ) is negative at
  • is some control (e.g., possibly extreme, like "off" or "reverse") that ensures Equation (5) (i.e., ) is positive at
The resulting trajectory should move toward the sliding surface where . Because real systems have delay, sliding mode trajectories often chatter back and forth along this sliding surface (i.e., the true trajectory may not smoothly follow, but it will always return to the sliding mode after leaving it).
  • Consider the dynamic system
which can be expressed in a 2-dimensional state space (with and ) as
\begin{cases} \dot{x}_1 = x_2\\ \dot{x}_2 = a(t,x_1,x_2) + u \end{cases}
Also assume that (i.e., has a finite upper bound that is known). For this system, choose the switching function
By the previous example, we must choose the feedback control law so that . Here,
  • When (i.e., when ), to make, the control law should be picked so that
  • When (i.e., when ), to make, the control law should be picked so that
However, by the triangle inequality,
and by the assumption about ,
So the system can be feedback stabilized (to return to the sliding mode) by means of the control law
u(x,\dot{x}) = \begin{cases} |\dot{x}| + k + 1 &\text{if } \underbrace{x + \dot{x}} < 0,\\ -\left(|\dot{x}| + k + 1\right) &\text{if } \overbrace{x + \dot{x}}^{\sigma} > 0 \end{cases}
which can be expressed in closed form as
Assuming that the system trajectories are forced to move so that, then
So once the system reaches the sliding mode, the system's 2-dimensional dynamics behave like this 1-dimensional system, which has a globally exponentially stable equilibrium at .

Read more about this topic:  Sliding Mode Control

Famous quotes containing the words control, design and/or examples:

    “To try to control a nine-month-old’s clinginess by forcing him away is a mistake, because it counteracts a normal part of the child’s development. To think that the child is clinging to you because he is spoiled is nonsense. Clinginess is not a discipline issue, at least not in the sense of correcting a wrongdoing.”
    —Lawrence Balter (20th century)

    “I begin with a design for a hearse.
    For Christ’s sake not black—
    nor white either—and not polished!
    Let it be weathered—like a farm wagon—”
    —William Carlos Williams (1883–1963)

    “No rules exist, and examples are simply life-savers answering the appeals of rules making vain attempts to exist.”
    —André Breton (1896–1966)