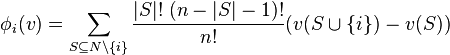Formal Definition
To formalize this situation, we use the notion of a coalitional game: we start out with a set N (of n players) and a function with, where denotes the empty set. The function that maps subsets of players to reals is called a characteristic function.
The function has the following meaning: if S is a coalition of players, then v(S), called the worth of coalition S, describes the total expected sum of payoffs the members of can obtain by cooperation.
The Shapley value is one way to distribute the total gains to the players, assuming that they all collaborate. It is a "fair" distribution in the sense that it is the only distribution with certain desirable properties to be listed below. According to the Shapley value, the amount that player i gets given a coalitional game is
where n is the total number of players and the sum extends over all subsets S of N not containing player i. The formula can be interpreted as follows. Imagine the coalition being formed one actor at a time, with each actor demanding their contribution v(S∪{i}) − v(S) as a fair compensation, and then averaging over the possible different permutations in which the coalition can be formed.
An alternative equivalent formula for the Shapley value is:
where the sum ranges over all orders of the players and is the set of players in which precede in the order .
Read more about this topic: Shapley Value
Famous quotes containing the words formal and/or definition:
“True variety is in that plenitude of real and unexpected elements, in the branch charged with blue flowers thrusting itself, against all expectations, from the springtime hedge which seems already too full, while the purely formal imitation of variety ... is but void and uniformity, that is, that which is most opposed to variety....”
—Marcel Proust (1871–1922)
“I’m beginning to think that the proper definition of “Man” is “an animal that writes letters.””
—Lewis Carroll [Charles Lutwidge Dodgson] (1832–1898)