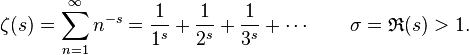Definition
The Riemann zeta function ζ(s) is a function of a complex variable s = σ + it (here, s, σ and t are traditional notations associated with the study of the ζ-function). The following infinite series converges for all complex numbers s with real part greater than 1, and defines ζ(s) in this case:
The Riemann zeta function is defined as the analytic continuation of the function defined for σ > 1 by the sum of the preceding series.
Leonhard Euler considered the above series in 1740 for positive integer values of s, and later Chebyshev extended the definition to real s > 1.
The above series is a prototypical Dirichlet series that converges absolutely to an analytic function for s such that σ > 1 and diverges for all other values of s. Riemann showed that the function defined by the series on the half-plane of convergence can be continued analytically to all complex values s ≠ 1. For s = 1 the series is the harmonic series which diverges to +∞, and
Thus the Riemann zeta function is a meromorphic function on the whole complex s-plane, which is holomorphic everywhere except for a simple pole at s = 1 with residue 1.
Read more about this topic: Riemann Zeta Function
Famous quotes containing the word definition:
“It is very hard to give a just definition of love. The most we can say of it is this: that in the soul, it is a desire to rule; in the spirit, it is a sympathy; and in the body, it is but a hidden and subtle desire to possess—after many mysteries—what one loves.”
—François, Duc De La Rochefoucauld (1613–1680)
“Perhaps the best definition of progress would be the continuing efforts of men and women to narrow the gap between the convenience of the powers that be and the unwritten charter.”
—Nadine Gordimer (b. 1923)
“It’s a rare parent who can see his or her child clearly and objectively. At a school board meeting I attended . . . the only definition of a gifted child on which everyone in the audience could agree was “mine.””
—Jane Adams (20th century)