Resolution (logic) - A Simple Example

A Simple Example

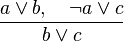
$\frac{a \vee b, \quad \neg a \vee c} {b \vee c}$

In plain language: Suppose is false. In order for the premise to be true, must be true. Alternatively, suppose is true. In order for the premise to be true, must be true. Therefore regardless of falsehood or veracity of, if both premises hold, then the conclusion is true.

Read more about this topic: Resolution (logic)

Famous quotes containing the word simple:

“I ... observed the great beauty of American government to be, that the simple machines of representation, carried through all its parts, gives facility for a being moulded at will to fit with the knowledge of the age; that thus, although it should be imperfect in any or all of its parts, it bears within it a perfect principle the principle of improvement.
”
—Frances Wright (1795–1852)