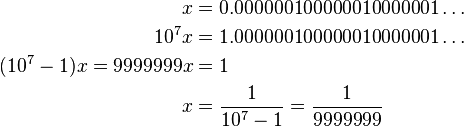Repeating Decimal - Converting Repeating Decimals To Fractions - A Shortcut

A Shortcut

The above argument can be applied in particular if the repeating sequence has n digits, all of which are 0 except the final one which is 1. For instance for n = 7:

So this particular repeating decimal corresponds to the fraction 1/(10n − 1), where the denominator is the number written as n digits 9. Knowing just that, a general repeating decimal can be expressed as a fraction without having to solve an equation. For example, one could reason:

It is possible to get a general formula expressing a repeating decimal with an n digit period, beginning right after the decimal point, as a fraction:

x = 0.(A₁A₂…A_n)

10nx = A₁A₂…A_n.(A₁A₂…A_n)

(10n - 1)x = 99…99x = A₁A₂…A_n

x = A₁A₂…A_n/(10n - 1)

= A₁A₂…A_n/99…99

More explicitly one gets the following cases.

If the repeating decimal is between 0 and 1, and the repeating block is n digits long, first occurring right after the decimal point, then the fraction (not necessarily reduced) will be the integer number represented by the n-digit block divided by the one represented by n digits 9. For example,

• 0.444444… = 4/9 since the repeating block is 4 (a 1-digit block),
• 0.565656… = 56/99 since the repeating block is 56 (a 2-digit block),
• 0.012012… = 12/999 since the repeating block is 012 (a 3-digit block), and this further reduces to 4/333.
• 0.9999999… = 9/9 = 1, since the repeating block is 9 (also a 1-digit block)

If the repeating decimal is as above, except that there are k (extra) digits 0 between the decimal point and the repeating n-digit block, then one can simply add k digits 0 after the n digits 9 of the denominator (and as before the fraction may subsequently be simplified). For example,

• 0.000444… = 4/9000 since the repeating block is 4 and this block is preceded by 3 zeros,
• 0.005656… = 56/9900 since the repeating block is 56 and it is preceded by 2 zeros,
• 0.00012012… = 12/99900 = 2/16650 since the repeating block is 012 and it is preceded by 2 (!) zeros.

Any repeating decimal not of the form described above can be written as a sum of a terminating decimal and a repeating decimal of one of the two above types (actually the first type suffices, but that could require the terminating decimal to be negative). For example,

• 1.23444… = 1.23 + 0.00444… = 123/100 + 4/900 = 1107/900 + 4/900 = 1111/900 or alternatively 1.23444… = 0.79 + 0.44444… = 79/100 + 4/9 = 711/900 + 400/900 = 1111/900
• 0.3789789… = 0.3 + 0.0789789… = 3/10 + 789/9990 = 2997/9990 + 789/9990 = 3786/9990 = 631/1665 or alternatively 0.3789789… = −0.6 + 0.9789789… = −6/10 + 978/999 = −5994/9990 + 9780/9990 = 3786/9990 = 631/1665

It follows that any repeating decimal with period n, and k digits after the decimal point that do not belong to the repeating part, can be written as a (not necessarily reduced) fraction whose denominator is (10n − 1)10k.

Conversely the period of the repeating decimal of a fraction c/d will be (at most) the smallest number n such that 10n − 1 is divisible by d.

For example, the fraction 2/7 has d = 7, and the smallest k that makes 10k − 1 divisible by 7 is k = 6, because 999999 = 7 × 142857. The period of the fraction 2/7 is therefore 6.