Elements of RG Theory
In more technical terms, let us assume that we have a theory described by a certain function of the state variables and a certain set of coupling constants . This function may be a partition function, an action, a Hamiltonian, etc. It must contain the whole description of the physics of the system.
Now we consider a certain blocking transformation of the state variables, the number of must be lower than the number of . Now let us try to rewrite the function only in terms of the . If this is achievable by a certain change in the parameters,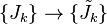 
, then the theory is said to be renormalizable.
For some reason, most fundamental theories of physics such as quantum electrodynamics, quantum chromodynamics and electro-weak interaction, but not gravity, are exactly renormalizable. Also, most theories in condensed matter physics are approximately renormalizable, from superconductivity to fluid turbulence.
The change in the parameters is implemented by a certain beta function: 
, which is said to induce a renormalization flow (or RG flow) on the -space. The values of under the flow are called running couplings.
As was stated in the previous section, the most important information in the RG flow are its fixed points. The possible macroscopic states of the system, at a large scale, are given by this set of fixed points.
Since the RG transformations in such systems are lossy (i.e.: the number of variables decreases - see as an example in a different context, Lossy data compression), there need not be an inverse for a given RG transformation. Thus, in such lossy systems, the renormalization group is, in fact, a semigroup.
Read more about this topic: Renormalization Group
Famous quotes containing the words elements of, elements and/or theory:
“The popularity of that baby-faced boy, who possessed not even the elements of a good actor, was a hallucination in the public mind, and a disgrace to our theatrical history.”
—Thomas Campbell (1777–1844)
“Three elements go to make up an idea. The first is its intrinsic quality as a feeling. The second is the energy with which it affects other ideas, an energy which is infinite in the here-and-nowness of immediate sensation, finite and relative in the recency of the past. The third element is the tendency of an idea to bring along other ideas with it.”
—Charles Sanders Peirce (1839–1914)
“A theory if you hold it hard enough
And long enough gets rated as a creed....”
—Robert Frost (1874–1963)