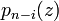Regular Singular Point - Formal Definitions

Formal Definitions

More precisely, consider an ordinary linear differential equation of n-th order

with p_i (z) meromorphic functions. One can assume that

If this is not the case the equation above has to be divided by p_n(x). This may introduce singular points to consider.

The equation should be studied on the Riemann sphere to include the point at infinity as a possible singular point. A Möbius transformation may be applied to move ∞ into the finite part of the complex plane if required, see example on Bessel differential equation below.

Then the Frobenius method based on the indicial equation may be applied to find possible solutions that are power series times complex powers (z − a)r near any given a in the complex plane where r need not be an integer; this function may exist, therefore, only thanks to a branch cut extending out from a, or on a Riemann surface of some punctured disc around a. This presents no difficulty for a an ordinary point (Lazarus Fuchs 1866). When a is a regular singular point, which by definition means that

has a pole of order at most i at a, the Frobenius method also can be made to work and provide n independent solutions near a.

Otherwise the point a is an irregular singularity. In that case the monodromy group relating solutions by analytic continuation has less to say in general, and the solutions are harder to study, except in terms of their asymptotic expansions.

The regularity condition is a kind of Newton polygon condition, in the sense that the allowed poles are in a region, when plotted against i, bounded by a line at 45° to the axes.

An ordinary differential equation whose only singular points, including the point at infinity, are regular singular points is called a Fuchsian ordinary differential equation.