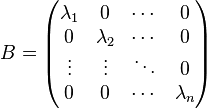Quadratic Form - Real Quadratic Forms

Real Quadratic Forms

See also: Sylvester's law of inertia and Definite form

Any n×n real symmetric matrix A determines a quadratic form q_A in n variables by the formula

Conversely, given a quadratic form in n variables, its coefficients can be arranged into an n×n symmetric matrix. One of the most important questions in the theory of quadratic forms is how much can one simplify a quadratic form q by a homogeneous linear change of variables. A fundamental theorem due to Jacobi asserts that q can be brought to a diagonal form

so that the corresponding symmetric matrix is diagonal, and this is even possible to accomplish with a change of variables given by an orthogonal matrix – in this case the coefficients λ₁, λ₂, …, λ_n are in fact determined uniquely up to a permutation. If the change of variables is given by an invertible matrix, not necessarily orthogonal, then the coefficients λ_i can be made to be 0,1, and −1. Sylvester's law of inertia states that the numbers of 1 and −1 are invariants of the quadratic form, in the sense that any other diagonalization will contain the same number of each. The signature of the quadratic form is the triple (n₀, n₊, n₋) where n₀ is the number 0s and n_± is the number of ±1s. Sylvester's law of inertia shows that this is a well-defined quantity attached to the quadratic form. The case when all λ_i have the same sign is especially important: in this case the quadratic form is called positive definite (all 1) or negative definite (all −1); if none of the terms are 0 then the form is called nondegenerate; this includes positive definite, negative definite, and indefinite (a mix of 1 and −1); equivalently, a nondegenerate quadratic form is one whose associated symmetric form is a nondegenerate bilinear form. A real vector space with an indefinite nondegenerate quadratic form of index (p,q) (p 1s, q −1s) is often denoted as Rp,q particularly in the physical theory of space-time.

The discriminant of a quadratic form, concretely the class of the determinant of a representing matrix in K/(K*)2 (up to non-zero squares) can also be defined, and for a real quadratic form is a cruder invariant than signature, taking values of only “positive, zero, or negative”. Zero corresponds to degenerate, while for a non-degenerate form it is the parity of the number of negative coefficients,

These results are reformulated in a different way below.

Let q be a quadratic form defined on an n-dimensional real vector space. Let A be the matrix of the quadratic form q in a given basis. This means that A is a symmetric n×n matrix such that

where x is the column vector of coordinates of v in the chosen basis. Under a change of basis, the column x is multiplied on the left by an n×n invertible matrix S, and the symmetric square matrix A is transformed into another symmetric square matrix B of the same size according to the formula

Any symmetric matrix A can be transformed into a diagonal matrix

by a suitable choice of an orthogonal matrix S, and the diagonal entries of B are uniquely determined — this is Jacobi's theorem. If S is allowed to be any invertible matrix then B can be made to have only 0,1, and −1 on the diagonal, and the number of the entries of each type (n₀ for 0, n₊ for 1, and n₋ for −1) depends only on A. This is one of the formulations of Sylvester's law of inertia and the numbers n₊ and n₋ are called the positive and negative indices of inertia. Although their definition involved a choice of basis and consideration of the corresponding real symmetric matrix A, Sylvester's law of inertia means that they are invariants of the quadratic form q.

The quadratic form q is positive definite (resp., negative definite) if q(v) > 0 (resp., q(v) < 0) for every nonzero vector v. When q(v) assumes both positive and negative values, q is an indefinite quadratic form. The theorems of Jacobi and Sylvester show that any positive definite quadratic form in n variables can be brought to the sum of n squares by a suitable invertible linear transformation: geometrically, there is only one positive definite real quadratic form of every dimension. Its isometry group is a compact orthogonal group O(n). This stands in contrast with the case of indefinite forms, when the corresponding group, the indefinite orthogonal group O(p, q), is non-compact. Further, the isometry groups of Q and −Q are the same (O(p, q) ≈ O(q, p)), but the associated Clifford algebras (and hence Pin groups) are different.