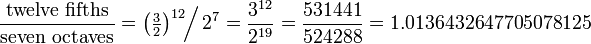Circle of Fifths and Enharmonic Change
The Pythagorean comma can also be thought of as the discrepancy between twelve justly tuned perfect fifths (ratio 3:2) ( play) and seven octaves (ratio 2:1):
|
|
In the following table of musical scales in the circle of fifths, the Pythagorean comma is visible as the small interval between e.g. F♯ and G♭.
The 6♭ and the 6♯ scales* are not identical - even though they are on the piano keyboard - but the ♭ scales are one Pythagorean comma lower. Disregarding this difference leads to enharmonic change.
This interval has serious implications for the various tuning schemes of the chromatic scale, because in Western music, 12 perfect fifths and seven octaves are treated as the same interval. Equal temperament, today the most common tuning system used in the West, reconciled this by flattening each fifth by a twelfth of a Pythagorean comma (approximately 2 cents), thus producing perfect octaves.
Another way to express this is that the just fifth has a frequency ratio (compared to the tonic) of 3:2 or 1.5 to 1, whereas the seventh semitone (based on 12 equal logarithmic divisions of an octave) is the seventh power of the twelfth root of two or 1.4983... to 1, which is not quite the same (out by about 0.1%). Take the just fifth to the twelfth power, then subtract seven octaves, and you get the Pythagorean comma (about 1.4% difference).
Read more about this topic: Pythagorean Comma
Famous quotes containing the words circle of, circle and/or change:
“Perchance we may,
Where now this night is day,
And even through faith of still averted feet,
Making full circle of our banishment,
Amazed meet;”
—Coventry Kersey Dighton Patmore (1823–1896)
“That three times five is equal to the half of thirty, expresses a relation between these numbers. Propositions of this kind are discoverable by the mere operation of thought, without dependence on what is any where existent in the universe. Though there never were a circle or triangle in nature, the truths, demonstrated by Euclid, would for ever retain their certainty and evidence.”
—David Hume (1711–1776)
“The personal things should be left out of platforms at conventions .... You can argue yourself blue in the face, and you’re not going to change each other’s minds. It’s a waste of your time and my time.”
—Barbara Bush (b. 1925)