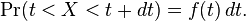Probability Density Function - Further Details

Further Details

Unlike a probability, a probability density function can take on values greater than one; for example, the uniform distribution on the interval has probability density f(x) = 2 for 0 ≤ x ≤ ½ and f(x) = 0 elsewhere.

The standard normal distribution has probability density

f(x) = \frac{1}{\sqrt{2\pi}}\; e^{-x^2/2}.

If a random variable X is given and its distribution admits a probability density function f, then the expected value of X (if it exists) can be calculated as

\operatorname{E} = \int_{-\infty}^\infty x\,f(x)\,dx.

Not every probability distribution has a density function: the distributions of discrete random variables do not; nor does the Cantor distribution, even though it has no discrete component, i.e., does not assign positive probability to any individual point.

A distribution has a density function if and only if its cumulative distribution function F(x) is absolutely continuous. In this case: F is almost everywhere differentiable, and its derivative can be used as probability density:

\frac{d}{dx}F(x) = f(x).

If a probability distribution admits a density, then the probability of every one-point set {a} is zero; the same holds for finite and countable sets.

Two probability densities f and g represent the same probability distribution precisely if they differ only on a set of Lebesgue measure zero.

In the field of statistical physics, a non-formal reformulation of the relation above between the derivative of the cumulative distribution function and the probability density function is generally used as the definition of the probability density function. This alternate definition is the following:

If dt is an infinitely small number, the probability that X is included within the interval (t, t + dt) is equal to f(t) dt, or:

\Pr(t<X<t+dt) = f(t)\,dt.

Read more about this topic:  Probability Density Function

Famous quotes containing the word details:

    “If my sons are to become the kind of men our daughters would be pleased to live among, attention to domestic details is critical. The hostilities that arise over housework...are crushing the daughters of my generation....Change takes time, but men’s continued obliviousness to home responsibilities is causing women everywhere to expire of trivialities.”
    —Mary Kay Blakely (20th century)

    “Anyone can see that to write Uncle Tom’s Cabin on the knee in the kitchen, with constant calls to cooking and other details of housework to punctuate the paragraphs, was a more difficult achievement than to write it at leisure in a quiet room.”
    —Anna Garlin Spencer (1851–1931)