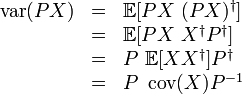Principal Component Analysis - Derivation of PCA Using The Covariance Method

Derivation of PCA Using The Covariance Method

Let X be a d-dimensional random vector expressed as column vector. Without loss of generality, assume X has zero mean.

We want to find a orthonormal transformation matrix P so that PX has a diagonal covariant matrix (i.e. PX is a random vector with all its distinct components pairwise uncorrelated).

A quick computation assuming were unitary yields:

\begin{array}{rcl} \operatorname{var}(PX) &= &\mathbb{E}\\ &= &\mathbb{E}\\ &= &P~\mathbb{E}P^{\dagger}\\ &= &P~\operatorname{cov}(X)P^{-1}\\ \end{array}

Hence holds if and only if were diagonalisable by .

This is very constructive, as var(X) is guaranteed to be a non-negative definite matrix and thus is guaranteed to be diagonalisable by some unitary matrix.

Read more about this topic:  Principal Component Analysis

Famous quotes containing the word method:

    “I have a new method of poetry. All you got to do is look over your notebooks ... or lay down on a couch, and think of anything that comes into your head, especially the miseries.... Then arrange in lines of two, three or four words each, don’t bother about sentences, in sections of two, three or four lines each.”
    —Allen Ginsberg (b. 1926)