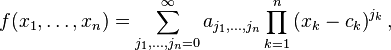Power Series - Power Series in Several Variables

Power Series in Several Variables

An extension of the theory is necessary for the purposes of multivariable calculus. A power series is here defined to be an infinite series of the form

f(x_1,\dots,x_n) = \sum_{j_1,\dots,j_n = 0}^{\infty}a_{j_1,\dots,j_n} \prod_{k=1}^n \left(x_k - c_k \right)^{j_k},

where j = (j1, ..., jn) is a vector of natural numbers, the coefficients a(j1,...,jn) are usually real or complex numbers, and the center c = (c1, ..., cn) and argument x = (x1, ..., xn) are usually real or complex vectors. In the more convenient multi-index notation this can be written

f(x) = \sum_{\alpha \in \mathbb{N}^n} a_{\alpha} \left(x - c \right)^{\alpha}.

The theory of such series is trickier than for single-variable series, with more complicated regions of convergence. For instance, the power series is absolutely convergent in the set between two hyperbolas. (This is an example of a log-convex set, in the sense that the set of points, where lies in the above region, is a convex set. More generally, one can show that when c=0, the interior of the region of absolute convergence is always a log-convex set in this sense.) On the other hand, in the interior of this region of convergence one may differentiate and integrate under the series sign, just as one may with ordinary power series.

Read more about this topic:  Power Series

Famous quotes containing the words power, series and/or variables:

    “I know not whether the remark is to our honour or otherwise, that lessons of wisdom have never such power over us, as when they are wrought into the heart, through the ground-work of a story which engages the passions: Is it that we are like iron, and must first be heated before we can be wrought upon?”
    —Laurence Sterne (1713–1768)

    “In the order of literature, as in others, there is no act that is not the coronation of an infinite series of causes and the source of an infinite series of effects.”
    —Jorge Luis Borges (1899–1986)

    “The variables of quantification, ‘something,’ ‘nothing,’ ‘everything,’ range over our whole ontology, whatever it may be; and we are convicted of a particular ontological presupposition if, and only if, the alleged presuppositum has to be reckoned among the entities over which our variables range in order to render one of our affirmations true.”
    —Willard Van Orman Quine (b. 1908)