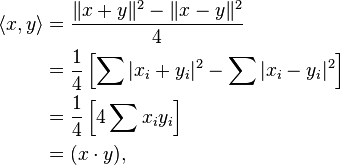Normed Vector Spaces Satisfying The Parallelogram Law
Most real and complex normed vector spaces do not have inner products, but all normed vector spaces have norms (by definition). For example, a commonly used norm is the p-norm:
where the are the components of vector .
Given a norm, one can evaluate both sides of the parallelogram law above. A remarkable fact is that if the parallelogram law holds, then the norm must arise in the usual way from some inner product. In particular, it holds for the p-norm if and only if p = 2, the so-called Euclidean norm or standard norm.
For any norm satisfying the parallelogram law (which necessarily is an inner product norm), the inner product generating the norm is unique as a consequence of the polarization identity. In the real case, the polarization identity is given by:
or, equivalently, by:
In the complex case it is given by:
For example, using the p-norm with p = 2 and real vectors, the evaluation of the inner product proceeds as follows:
which is the standard dot product of two vectors.
Read more about this topic: Parallelogram Law
Famous quotes containing the words spaces, satisfying and/or law:
“In any case, raw aggression is thought to be the peculiar province of men, as nurturing is the peculiar province of women.... The psychologist Erik Erikson discovered that, while little girls playing with blocks generally create pleasant interior spaces and attractive entrances, little boys are inclined to pile up the blocks as high as they can and then watch them fall down: “the contemplation of ruins,” Erikson observes, “is a masculine specialty.””
—Joyce Carol Oates (b. 1938)
“Persons who insist to themselves that under one set of conditions only can they lead interesting and satisfying lives lay themselves open to bitter disappointments and frustrations.”
—Hortense Odlum (1892–?)
“Will mankind never learn that policy is not morality,—that it never secures any moral right, but considers merely what is expedient? chooses the available candidate,—who is invariably the devil,—and what right have his constituents to be surprised, because the devil does not behave like an angel of light? What is wanted is men, not of policy, but of probity,—who recognize a higher law than the Constitution, or the decision of the majority.”
—Henry David Thoreau (1817–1862)