Mathematical Description
Let γ(s) be a regular parametric plane curve, where s is the arc length, or natural parameter. This determines the unit tangent vector T, the unit normal vector N, the signed curvature k(s) and the radius of curvature at each point:
Suppose that P is a point on C where k ≠ 0. The corresponding center of curvature is the point Q at distance R along N, in the same direction if k is positive and in the opposite direction if k is negative. The circle with center at Q and with radius R is called the osculating circle to the curve C at the point P.
If C is a regular space curve then the osculating circle is defined in a similar way, using the principal normal vector N. It lies in the osculating plane, the plane spanned by the tangent and principal normal vectors T and N at the point P.
The plane curve can also be given in a different regular parametrization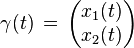 
where regular means that for all . Then the formulas for the signed curvature k(t), the normal unit vector N(t), the radius of curvature R(t), and the center Q(t) of the osculating cicle are
- ,
Read more about this topic: Osculating Circle
Famous quotes containing the words mathematical and/or description:
“As we speak of poetical beauty, so ought we to speak of mathematical beauty and medical beauty. But we do not do so; and that reason is that we know well what is the object of mathematics, and that it consists in proofs, and what is the object of medicine, and that it consists in healing. But we do not know in what grace consists, which is the object of poetry.”
—Blaise Pascal (1623–1662)
“Everything to which we concede existence is a posit from the standpoint of a description of the theory-building process, and simultaneously real from the standpoint of the theory that is being built. Nor let us look down on the standpoint of the theory as make-believe; for we can never do better than occupy the standpoint of some theory or other, the best we can muster at the time.”
—Willard Van Orman Quine (b. 1908)