Newtonian Dynamics - Relation To Lagrange Equations

Relation To Lagrange Equations

Mechanical systems with constraints are usually described by Lagrange equations:

\frac{dq^s}{dt}=w^s,\qquad\frac{d}{dt}\left(\frac{\partial T}{\partial w^s}\right)-\frac{\partial T}{\partial q^s}=Q_s,\qquad s=1,\,\ldots,\,n,

(16)

where is the kinetic energy the constrained dynamical system given by the formula (12). The quantities in (16) are the inner covariant components of the tangent force vector (see (13) and (14)). They are produced from the inner contravariant components of the vector by means of the standard index lowering procedure using the metric (11):

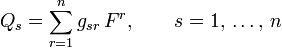Q_s=\sum^n_{r=1}g_{sr}\,F^r,\qquad s=1,\,\ldots,\,n,

(17)

The equations (16) are equivalent to the equations (15). However, the metric (11) and other geometric features of the configuration manifold are not explicit in (16). The metric (11) can be recovered from the kinetic energy by means of the formula

g_{ij}=\frac{\partial^2T}{\partial w^i\,\partial w^j}.

(18)

Read more about this topic:  Newtonian Dynamics

Famous quotes containing the words relation to and/or relation:

    “Light is meaningful only in relation to darkness, and truth presupposes error. It is these mingled opposites which people our life, which make it pungent, intoxicating. We only exist in terms of this conflict, in the zone where black and white clash.”
    —Louis Aragon (1897–1982)

    “The foregoing generations beheld God and nature face to face; we, through their eyes. Why should not we also enjoy an original relation to the universe? Why should not we have a poetry and philosophy of insight and not of tradition, and a religion by revelation to us, and not the history of theirs?”
    —Ralph Waldo Emerson (1803–1882)