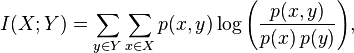Mutual Information - Definition of Mutual Information

Definition of Mutual Information

Formally, the mutual information of two discrete random variables X and Y can be defined as:

I(X;Y) = \sum_{y \in Y} \sum_{x \in X} p(x,y) \log{ \left(\frac{p(x,y)}{p(x)\,p(y)} \right) }, \,\!

where p(x,y) is the joint probability distribution function of X and Y, and and are the marginal probability distribution functions of X and Y respectively.

In the case of continuous random variables, the summation is replaced by a definite double integral:

I(X;Y) = \int_Y \int_X p(x,y) \log{ \left(\frac{p(x,y)}{p(x)\,p(y)} \right) } \; dx \,dy,

where p(x,y) is now the joint probability density function of X and Y, and and are the marginal probability density functions of X and Y respectively.

These definitions are ambiguous because the base of the log function is not specified. To disambiguate, the function I could be parameterized as I(X,Y,b) where b is the base. Alternatively, since the most common unit of measurement of mutual information is the bit, a base of 2 could be specified.

Intuitively, mutual information measures the information that X and Y share: it measures how much knowing one of these variables reduces uncertainty about the other. For example, if X and Y are independent, then knowing X does not give any information about Y and vice versa, so their mutual information is zero. At the other extreme, if X and Y are identical then all information conveyed by X is shared with Y: knowing X determines the value of Y and vice versa. As a result, in the case of identity the mutual information is the same as the uncertainty contained in Y (or X) alone, namely the entropy of Y (or X: clearly if X and Y are identical they have equal entropy).

Mutual information is a measure of the inherent dependence expressed in the joint distribution of X and Y relative to the joint distribution of X and Y under the assumption of independence. Mutual information therefore measures dependence in the following sense: I(X; Y) = 0 if and only if X and Y are independent random variables. This is easy to see in one direction: if X and Y are independent, then p(x,y) = p(x) p(y), and therefore:

\log{ \left( \frac{p(x,y)}{p(x)\,p(y)} \right) } = \log 1 = 0. \,\!

Moreover, mutual information is nonnegative (i.e. I(X;Y) ≥ 0; see below) and symmetric (i.e. I(X;Y) = I(Y;X)).

Read more about this topic:  Mutual Information

Famous quotes containing the words definition of, definition, mutual and/or information:

    “The very definition of the real becomes: that of which it is possible to give an equivalent reproduction.... The real is not only what can be reproduced, but that which is always already reproduced. The hyperreal.”
    —Jean Baudrillard (b. 1929)

    “I’m beginning to think that the proper definition of “Man” is “an animal that writes letters.””
    —Lewis Carroll [Charles Lutwidge Dodgson] (1832–1898)

    “We call it a Society; and go about professing openly the totalest separation, isolation. Our life is not a mutual helpfulness; but rather, cloaked under due laws-of-war, named “fair competition” and so forth, it is a mutual hostility.”
    —Thomas Carlyle (1795–1881)

    “When action grows unprofitable, gather information; when information grows unprofitable, sleep.”
    —Ursula K. Le Guin (b. 1929)