Lists of Integrals - Definite Integrals Lacking Closed-form Antiderivatives

Definite Integrals Lacking Closed-form Antiderivatives

There are some functions whose antiderivatives cannot be expressed in closed form. However, the values of the definite integrals of some of these functions over some common intervals can be calculated. A few useful integrals are given below.

(see also Gamma function)
(the Gaussian integral)
for a > 0
\int_0^\infty x^{2n} e^{-a x^2}\,dx = \frac{2n-1}{2a} \int_0^\infty x^{2(n-1)} e^{-a x^2}\,dx = \frac{(2n-1)!!}{2^{n+1}} \sqrt{\frac{\pi}{a^{2n+1}}} = \frac{(2n)!}{n! 2^{2n+1}} \sqrt{\frac{\pi}{a^{2n+1}}} for a > 0, n is 1, 2, 3, ... and !! is the double factorial.
when a > 0
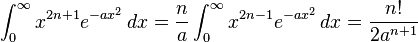\int_0^\infty x^{2n+1} e^{-a x^2}\,dx = \frac {n} {a} \int_0^\infty x^{2n-1} e^{-a x^2}\,dx = \frac{n!}{2 a^{n+1}} for a > 0, n = 0, 1, 2, ....
(see also Bernoulli number)
(see sinc function and Sine integral)
(if n is an even integer and )
(if is an odd integer and )
\int_{-\pi}^\pi \cos(\alpha x)\cos^n(\beta x) dx = \begin{cases} \frac{2 \pi}{2^n} \binom{n}{m} & |\alpha|= |\beta (2m-n)| \\ 0 & \text{otherwise} \end{cases} (for integers with and, see also Binomial coefficient)
(for real and non-negative integer, see also Symmetry)
\int_{-\pi}^\pi \sin(\alpha x) \sin^n(\beta x) dx = \begin{cases} (-1)^{(n+1)/2} (-1)^m \frac{2 \pi}{2^n} \binom{n}{m} & n \text{ odd},\ \alpha = \beta (2m-n) \\ 0 & \text{otherwise} \end{cases} (for integers with and, see also Binomial coefficient)
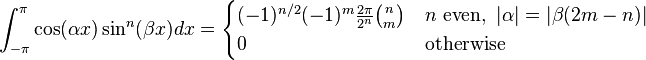\int_{-\pi}^{\pi} \cos(\alpha x) \sin^n(\beta x) dx = \begin{cases} (-1)^{n/2} (-1)^m \frac{2 \pi}{2^n} \binom{n}{m} & n \text{ even},\ |\alpha| = |\beta (2m-n)| \\ 0 & \text{otherwise} \end{cases} (for integers with and, see also Binomial coefficient)
(where is the exponential function, and )
(where is the Gamma function)
(the Beta function)
(where is the modified Bessel function of the first kind)
, this is related to the probability density function of the Student's t-distribution)

The method of exhaustion provides a formula for the general case when no antiderivative exists:

(Click "show" at right to see a proof or "hide" to hide it.)

Read more about this topic:  Lists Of Integrals

Famous quotes containing the words definite and/or lacking:

    “White ... is not a mere absence of colour; it is a shining and affirmative thing, as fierce as red, as definite as black.... God paints in many colours; but He never paints so gorgeously, I had almost said so gaudily, as when He paints in white.”
    —Gilbert Keith Chesterton (1874–1936)

    “I should consent to breed under pressure, if I were convinced in any way of the reasonableness of reproducing the species. But my nerves and the nerves of any woman I could live with three months, would produce only a victim ... lacking in impulse, a mere bundle of discriminations. If I were wealthy I might subsidize a stud of young peasants, or a tribal group in Tahiti.”
    —Ezra Pound (1885–1972)