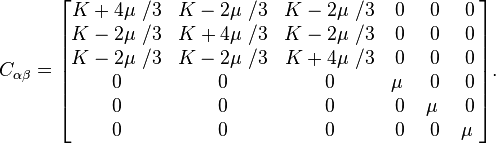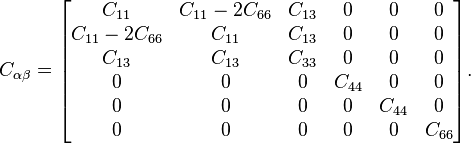Linear Elasticity - Anisotropic Homogeneous Media

Anisotropic Homogeneous Media

For anisotropic media, the stiffness tensor is more complicated. The symmetry of the stress tensor means that there are at most 6 different elements of stress. Similarly, there are at most 6 different elements of the strain tensor . Hence the 4th rank stiffness tensor may be written as a 2nd rank matrix . Voigt notation is the standard mapping for tensor indices,

\begin{matrix} ij & =\\ \Downarrow & \\ \alpha & = \end{matrix} \begin{matrix} 11 & 22 & 33 & 23,32 & 13,31 & 12,21 \\ \Downarrow & \Downarrow & \Downarrow & \Downarrow & \Downarrow & \Downarrow & \\ 1 &2 & 3 & 4 & 5 & 6 \end{matrix}\,\!

With this notation, one can write the elasticity matrix for any linearly elastic medium as:

C_{ijkl} \Rightarrow C_{\alpha \beta} =\begin{bmatrix} C_{11} & C_{12} & C_{13} & C_{14} & C_{15} & C_{16} \\ C_{12} & C_{22} & C_{23} & C_{24} & C_{25} & C_{26} \\ C_{13} & C_{23} & C_{33} & C_{34} & C_{35} & C_{36} \\ C_{14} & C_{24} & C_{34} & C_{44} & C_{45} & C_{46} \\ C_{15} & C_{25} & C_{35} & C_{45} & C_{55} & C_{56} \\ C_{16} & C_{26} & C_{36} & C_{46} & C_{56} & C_{66} \end{bmatrix}. \,\!

As shown, the matrix is symmetric, because of the linear relation between stress and strain. Hence, there are at most 21 different elements of .

The isotropic special case has 2 independent elements:

C_{\alpha \beta} =\begin{bmatrix} K+4 \mu\ /3 & K-2 \mu\ /3 & K-2 \mu\ /3 & 0 & 0 & 0 \\ K-2 \mu\ /3 & K+4 \mu\ /3 & K-2 \mu\ /3 & 0 & 0 & 0 \\ K-2 \mu\ /3 & K-2 \mu\ /3 & K+4 \mu\ /3 & 0 & 0 & 0 \\ 0 & 0 & 0 & \mu\ & 0 & 0 \\ 0 & 0 & 0 & 0 & \mu\ & 0 \\ 0 & 0 & 0 & 0 & 0 & \mu\ \end{bmatrix}. \,\!

The simplest anisotropic case, that of cubic symmetry has 3 independent elements:

C_{\alpha \beta} =\begin{bmatrix} C_{11} & C_{12} & C_{12} & 0 & 0 & 0 \\ C_{12} & C_{11} & C_{12} & 0 & 0 & 0 \\ C_{12} & C_{12} & C_{11} & 0 & 0 & 0 \\ 0 & 0 & 0 & C_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & C_{44} & 0 \\ 0 & 0 & 0 & 0 & 0 & C_{44} \end{bmatrix}. \,\!

The case of transverse isotropy, also called polar anisotropy, (with a single axis (the 3-axis) of symmetry) has 5 independent elements:

C_{\alpha \beta} =\begin{bmatrix} C_{11} & C_{11}-2C_{66} & C_{13} & 0 & 0 & 0 \\ C_{11}-2C_{66} & C_{11} & C_{13} & 0 & 0 & 0 \\ C_{13} & C_{13} & C_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & C_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & C_{44} & 0 \\ 0 & 0 & 0 & 0 & 0 & C_{66} \end{bmatrix}. \,\!

When the transverse isotropy is weak (i.e. close to isotropy), an alternative parametrization utilizing Thomsen parameters, is convenient for the formulas for wave speeds.

The case of orthotropy (the symmetry of a brick) has 9 independent elements:

C_{\alpha \beta} =\begin{bmatrix} C_{11} & C_{12} & C_{13} & 0 & 0 & 0 \\ C_{12} & C_{22} & C_{23} & 0 & 0 & 0 \\ C_{13} & C_{23} & C_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & C_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & C_{55} & 0 \\ 0 & 0 & 0 & 0 & 0 & C_{66} \end{bmatrix}. \,\!

Read more about this topic:  Linear Elasticity

Famous quotes containing the words homogeneous and/or media:

    “O my Brothers! love your Country. Our Country is our home, the home which God has given us, placing therein a numerous family which we love and are loved by, and with which we have a more intimate and quicker communion of feeling and thought than with others; a family which by its concentration upon a given spot, and by the homogeneous nature of its elements, is destined for a special kind of activity.”
    —Giuseppe Mazzini (1805–1872)

    “One can describe a landscape in many different words and sentences, but one would not normally cut up a picture of a landscape and rearrange it in different patterns in order to describe it in different ways. Because a photograph is not composed of discrete units strung out in a linear row of meaningful pieces, we do not understand it by looking at one element after another in a set sequence. The photograph is understood in one act of seeing; it is perceived in a gestalt.”
    —Joshua Meyrowitz, U.S. educator, media critic. “The Blurring of Public and Private Behaviors,” No Sense of Place: The Impact of Electronic Media on Social Behavior, Oxford University Press (1985)