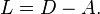Laplacian Matrix - Definition

Definition

Given a simple graph G with n vertices, its Laplacian matrix is defined as:

L = D - A.

That is, it is the difference of the degree matrix D and the adjacency matrix A of the graph. In the case of directed graphs, either the indegree or outdegree might be used, depending on the application.

From the definition follows that:

\ell_{i,j}:= \begin{cases} \deg(v_i) & \mbox{if}\ i = j \\ -1 & \mbox{if}\ i \neq j\ \mbox{and}\ v_i \mbox{ is adjacent to } v_j \\ 0 & \mbox{otherwise} \end{cases}

where deg(vi) is degree of the vertex i.

The normalized Laplacian matrix is defined as:

\ell_{i,j}:= \begin{cases} 1 & \mbox{if}\ i = j\ \mbox{and}\ \deg(v_i) \neq 0\\ -\frac{1}{\sqrt{\deg(v_i)\deg(v_j)}} & \mbox{if}\ i \neq j\ \mbox{and}\ v_i \mbox{ is adjacent to } v_j \\ 0 & \mbox{otherwise}. \end{cases}

Read more about this topic:  Laplacian Matrix

Famous quotes containing the word definition:

    “Although there is no universal agreement as to a definition of life, its biological manifestations are generally considered to be organization, metabolism, growth, irritability, adaptation, and reproduction.”
    —The Columbia Encyclopedia, Fifth Edition, the first sentence of the article on “life” (based on wording in the First Edition, 1935)

    “It’s a rare parent who can see his or her child clearly and objectively. At a school board meeting I attended . . . the only definition of a gifted child on which everyone in the audience could agree was “mine.””
    —Jane Adams (20th century)

    “One definition of man is “an intelligence served by organs.””
    —Ralph Waldo Emerson (1803–1882)