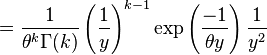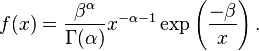Inverse-gamma Distribution - Derivation From Gamma Distribution

Derivation From Gamma Distribution

The pdf of the gamma distribution is

and define the transformation then the resulting transformation is

f_Y(y) = f_X \left( g^{-1}(y) \right) \left| \frac{d}{dy} g^{-1}(y) \right|
= \frac{1}{\theta^k \Gamma(k)} \left( \frac{1}{y} \right)^{k-1} \exp \left( \frac{-1}{\theta y} \right) \frac{1}{y^2}
= \frac{1}{\theta^k \Gamma(k)} \left( \frac{1}{y} \right)^{k+1} \exp \left( \frac{-1}{\theta y} \right)
= \frac{1}{\theta^k \Gamma(k)} y^{-k-1} \exp \left( \frac{-1}{\theta y} \right).

Replacing with ; with ; and with results in the inverse-gamma pdf shown above

f(x) = \frac{\beta^\alpha}{\Gamma(\alpha)} x^{-\alpha-1} \exp \left( \frac{-\beta}{x} \right).

Read more about this topic:  Inverse-gamma Distribution

Famous quotes containing the word distribution:

    “Classical and romantic: private language of a family quarrel, a dead dispute over the distribution of emphasis between man and nature.”
    —Cyril Connolly (1903–1974)