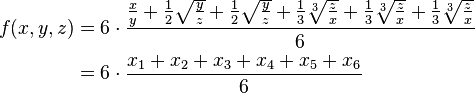Example Application
Consider the function
for all positive real numbers x, y and z. Suppose we wish to find the minimal value of this function. First we rewrite it a bit:
with
Applying the AM–GM inequality for n = 6, we get
Further, we know that the two sides are equal exactly when all the terms of the mean are equal:
All the points (x,y,z) satisfying these conditions lie on a half-line starting at the origin and are given by
Read more about this topic: Inequality Of Arithmetic And Geometric Means
Famous quotes containing the word application:
“It is known that Whistler when asked how long it took him to paint one of his “nocturnes” answered: “All of my life.” With the same rigor he could have said that all of the centuries that preceded the moment when he painted were necessary. From that correct application of the law of causality it follows that the slightest event presupposes the inconceivable universe and, conversely, that the universe needs even the slightest of events.”
—Jorge Luis Borges (1899–1986)
“Courage is resistance to fear, mastery of fear—not absence of fear. Except a creature be part coward it is not a compliment to say it is brave; it is merely a loose application of the word. Consider the flea!—incomparably the bravest of all the creatures of God, if ignorance of fear were courage.”
—Mark Twain [Samuel Langhorne Clemens] (1835–1910)