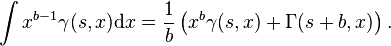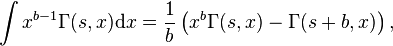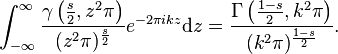Incomplete Gamma Function - Indefinite and Definite Integrals

Indefinite and Definite Integrals

The following indefinite integrals are readily obtained using integration by parts:

\int x^{b-1} \gamma(s,x) \mathrm d x = \frac{1}{b} \left( x^b \gamma(s,x) + \Gamma(s+b,x) \right).
\int x^{b-1} \Gamma(s,x) \mathrm d x = \frac{1}{b} \left( x^b \Gamma(s,x) - \Gamma(s+b,x) \right),

The lower and the upper incomplete Gamma function are connected via the Fourier transform:

\int_{-\infty}^\infty \frac {\gamma\left(\frac s 2, z^2 \pi \right)} {(z^2 \pi)^\frac s 2} e^{-2 \pi i k z} \mathrm d z = \frac {\Gamma\left(\frac {1-s} 2, k^2 \pi \right)} {(k^2 \pi)^\frac {1-s} 2}.

This follows, for example, by suitable specialization of (Gradshteyn & Ryzhik 1980, ยง 7.642).

Read more about this topic:  Incomplete Gamma Function

Famous quotes containing the words indefinite and/or definite:

    “... indefinite visions of ambition are weak against the ease of doing what is habitual or beguilingly agreeable.”
    —George Eliot [Mary Ann (or Marian)

    “Literature does not exist in a vacuum. Writers as such have a definite social function exactly proportional to their ability as writers. This is their main use.”
    —Ezra Pound (1885–1972)