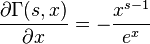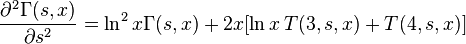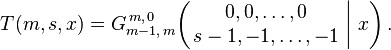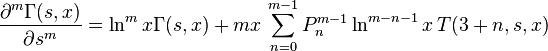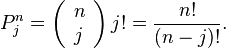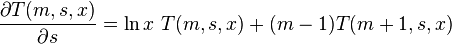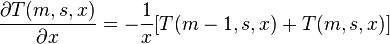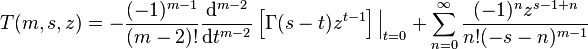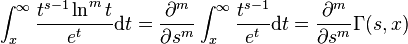Incomplete Gamma Function - Derivatives

Derivatives

The derivative of the upper incomplete gamma function with respect to x is well known. It is simply given by the integrand of its integral definition:

\frac{\partial \Gamma (s,x) }{\partial x} = - \frac{x^{s-1}}{e^x}

The derivative with respect to its first argument is given by

\frac{\partial \Gamma (s,x) }{\partial s} = \ln x \Gamma (s,x) + x\,T(3,s,x)

and the second derivative by

\frac{\partial^2 \Gamma (s,x) }{\partial s^2} = \ln^2 x \Gamma (s,x) + 2 x

where the function is a special case of the Meijer G-function

T(m,s,x) = G_{m-1,\,m}^{\,m,\,0} \!\left( \left. \begin{matrix} 0, 0, \dots, 0 \\ s-1, -1, \dots, -1 \end{matrix} \; \right| \, x \right).

This particular special case has internal closure properties of its own because it can be used to express all successive derivatives. In general,

\frac{\partial^m \Gamma (s,x) }{\partial s^m} = \ln^m x \Gamma (s,x) + m x\,\sum_{n=0}^{m-1} P_n^{m-1} \ln^{m-n-1} x\,T(3+n,s,x)

where

P_j^n = \left( \begin{array}{l} n \\ j \end{array} \right) j! = \frac{n!}{(n-j)!}.

All such derivatives can be generated in succession from:

\frac{\partial T (m,s,x) }{\partial s} = \ln x ~ T(m,s,x) + (m-1) T(m+1,s,x)

and

\frac{\partial T (m,s,x) }{\partial x} = -\frac{1}{x}

This function can be computed from its series representation valid for ,

T(m,s,z) = - \frac{(-1)^{m-1} }{(m-2)! } \frac{{\rm d}^{m-2} }{{\rm d}t^{m-2} } \left\Big|_{t=0} + \sum_{n=0}^{\infty} \frac{(-1)^n z^{s-1+n}}{n! (-s-n)^{m-1} }

with the understanding that s is not a negative integer or zero. In such a case, one must use a limit. Results for can be obtained by analytic continuation. Some special cases of this function can be simplified. For example, where is the Exponential integral. These derivatives and the function provide exact solutions to a number of integrals by repeated differentiation of the integral definition of the upper incomplete gamma function. For example,

\int_{x}^{\infty} \frac{t^{s-1} \ln^m t}{e^t} {\rm d}t= \frac{\partial^m}{\partial s^m} \int_{x}^{\infty} \frac{t^{s-1}}{e^t} {\rm d}t= \frac{\partial^m}{\partial s^m} \Gamma (s,x)

This formula can be further inflated or generalized to a huge class of Laplace transforms and Mellin transforms. When combined with a computer algebra system, the exploitation of special functions provides a powerful method for solving definite integrals, in particular those encountered by practical engineering applications (see Symbolic integration for more details).

Read more about this topic:  Incomplete Gamma Function